General relativity is a theory of gravitation
Nobel Prizes (3) - Albert Einstein, Pavel Cherenkov e Hendrik Lorentz
General relativity is a theory of gravitation developed by Einstein in the years 1907–1915. The development of general relativity began with the equivalence principle, under which the states of accelerated motion and being at rest in a gravitational field (for example when standing on the surface of the Earth) are physically identical.
 |
| Albert Einstein |
The upshot of this is that free fall is inertial motion: an object in free fall is falling because that is how objects move when there is no force being exerted on them, instead of this being due to the force of gravity as is the case in classical mechanics. This is incompatible with classical mechanics and special relativity because in those theories inertially moving objects cannot accelerate with respect to each other, but objects in free fall do so.
To resolve this difficulty Einstein first proposed that spacetime is curved. In 1915, he devised the Einstein field equations which relate the curvature of spacetime with the mass, energy, and momentum within it. Einstein's contemporaries did not all accept his new theories at once. However, the theory of relativity is now considered as a cornerstone of modern physics, see "Criticism of relativity theory".
Although it is widely acknowledged that Einstein was the creator of relativity in its modern understanding, some believe that others deserve credit for it, see Relativity priority dispute.
Advance of Mercury's Perihelion
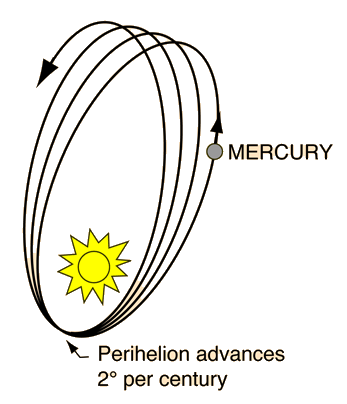 |
The perihelion of the orbit of the planet Mercury advances 2 degrees per century. 80 seconds of that advance was accounted for by perturbations from the other planets, etc., but the last 40 seconds of arc were unaccounted for. General relativity predicts an additional 43 seconds of arc and was one of the first triumphs of Einstein's theory.
The eccentricity of Mercury's orbit is exaggerated here to emphasize the effect.
|
Advance of Mercury's Perihelion
 | According to Roy D. North, more precise numbers are as follows (in arcsec per Julian century):
|
Gravitational Red Shift
According to the principle of equivalence from general relativity, any frequency shift which can be shown to arise from acceleration of a radiating source could also be produced by the appropriate gravitational field. Thus the expected shift in radiation frequency in a gravitational field can be related to the relativistic doppler shift experienced from an accelerating light source.
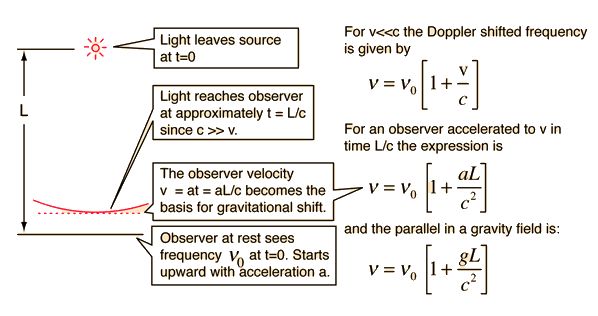
Gravitational Deflection of Light
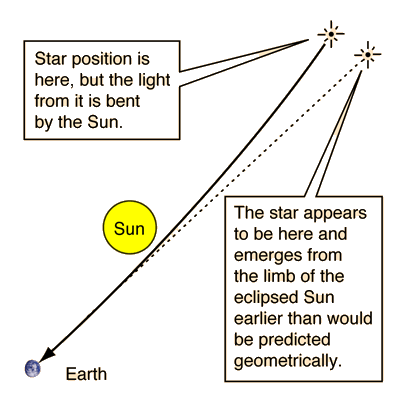 | Einstein's calculations in his newly developed general relativity indicated that the light from a star which just grazed the sun should be deflected by 1.75 seconds of arc. It was tested during the total eclipse of 1919 and during most of those which have ocurred since. |
This bending of light can produce a gravitational lensing effect if a distant galaxy or quasar is closely aligned with a massive galaxy closer to us. If one galaxy is directly behind another, the result can be a circle of light called an Einstein ring.
Black Hole
A black hole is an object so massive that even light cannot escape from it. This requires the idea of a gravitational mass for a photon, which then allows the calculation of an escape energy for an object of that mass. When the escape energy is equal to the photon energy, the implication is that the object is a "black hole".
Black Hole Conditions
After collapse to the neutron star stage, stars with masses less than 2-3 solar masses should remain neutron stars, gradually radiating away their energy, because there is no known mechanism for further combination, and forces between neutrons prevent further collapse. But this neutron force is the last stand, and our best calculations indicate that this repulsion which prevents collapse cannot withstand the gravity force of masses greater than 2 to 3 solar masses.
Such neutron stars would collapse toward zero spatial extent - toward a "singularity". Once they collapsed past a certain radius, the "event horizon", then even light could not escape: black hole. Since black holes by their very definition cannot be directly observed, proving their existence is difficult. The indirect evidence for the black hole Cygnus X-1 is a good example of the search for black holes.
The Schwarzschild Radius
Any mass can become a black hole if it collapses down to the Schwarzschild radius - but if a mass is over some critical value between 2 and 3 solar masses and has no fusion process to keep it from collapsing, then gravitational forces alone make the collapse to a black hole inevitable. Down past electron degeneracy, on past neutron degeneracy and then on past the Schwarzchild radius to collapse toward zero spatial extent - the singularity. The Schwarzschild radius (event horizon) just marks the radius of a sphere past which we can get no particles, no light, no information.
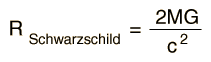
Gravity and the Photon
The relativistic energy expression attributes a mass to any energetic particle, and for the photon
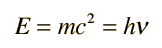
The gravitational potential energy is then
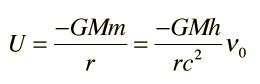
When the photon escapes the gravity field, it will have a different frequency
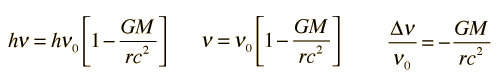
Since it is reduced in frequency, this is called the gravitational red shift or the Einstein red shift.
Escape Energy for Photon
If the gravitational potential energy of the photon is exactly equal to the photon energy then
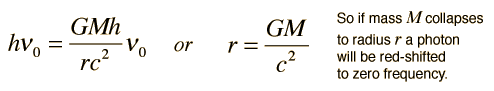
Note that this condition is independent of the frequency, and for a given mass M establishes a critical radius. Actually, Schwarzchilds's calculated gravitational radius differs from this result by a factor of 2 and is coincidently equal to the non-relativistic escape velocity expression
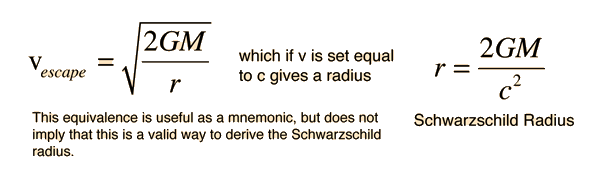
Harvard Tower Experiment
 | In just 22.6 meters, the fractional gravitational red shift given by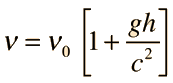
is just 4.92 x 10-15 , but the Mossbauer effect with the 14.4 keV gamma ray from iron-57 has a high enough resolution to detect that difference. In the early 60's physicists Pound, Rebka,and Snyder at the Jefferson Physical Laboratory at Harvard measured the shift to within 1% of the predicted shift.
|
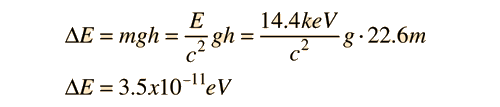

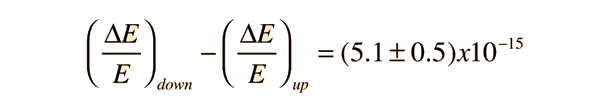
The success of this experiment owed much to the care of Pound and Rebka in preparing the source. They electroplated cobalt-57 onto the surface of a thin sheet of iron and then heated the combination at 1220 K for an hour.
The heat treatment caused the cobalt to diffuse into the iron to a depth of about 300 nm or 1000 atomic spacings. The source was then mounted on the cone of a loudspeaker driven at 10Hz to sweep the source velocity in a sinusoidal variation. The detector was a thin sheet of iron about 14 micrometers thick which was also annealed. The heat treatments were found to be crucial in obtaining high resolution.
Scout Rocket Experiment
I
n 1976 the Smithsonian Astrophysical Observatory sent aloft a Scout rocket to a height of 10,000 km. At this height, a clock should run 4.5 parts in 1010faster than one on the Earth. During two hours of free fall from its maximum height, the rocket transmitted timing pulses from a maser oscillator which acted as a clock and which was compared with a similar clock on the ground. This result confirmed the gravitational time dilation relationship to within 0.01%.
n 1976 the Smithsonian Astrophysical Observatory sent aloft a Scout rocket to a height of 10,000 km. At this height, a clock should run 4.5 parts in 1010faster than one on the Earth. During two hours of free fall from its maximum height, the rocket transmitted timing pulses from a maser oscillator which acted as a clock and which was compared with a similar clock on the ground. This result confirmed the gravitational time dilation relationship to within 0.01%.
Relativistic Mechanical Quantities
A number of ordinary mechanical quantities take on a different form as the speed approaches the speed of light.
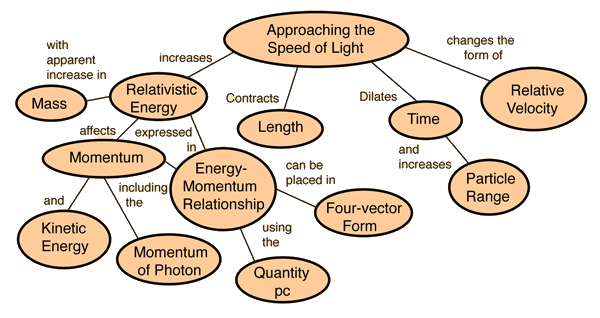
Einstein Velocity Addition
The relative velocity of any two objects never exceeds the velocity of light. Applying the Lorentz transformation to the velocities, expressions are obtained for the relative velocities as seen by the different observers. They are called the Einstein velocity addition relationships.
Atomic Fine Structure
One of the great successes of the quantum theory was the prediction of the energy levels of the hydrogen atom. When attempts were made to explain the fine structure of the hydrogen spectral lines, it was found that the splitting of the lines was in error by a factor of two. It was realized that relativistic time dilation must be used in calculating the frequencies, and calculations showed that this relativistic correction, called Thomas precession, was the factor of two which was needed for agreement with experiment.
Cerenkov Radiation
When highly radioactive objects are observed under water, such as in "swimming pool" reactors and in the underwater temporary spent fuel storage areas at nuclear reactors, they are seen to be bathed in an intense blue light called Cerenkov radiation. It is caused by particles entering the water at speeds greater than the speed of light in the water.
As the particles slow down to the local speed of light, they produce a cone of light roughly analogous to the bow wave of a boat which is moving through water at a speed greater than the wave speed on the surface of the water. Another analogy statement is to say that the Cerenkov cone is like a sonic boom except that it is done with light.
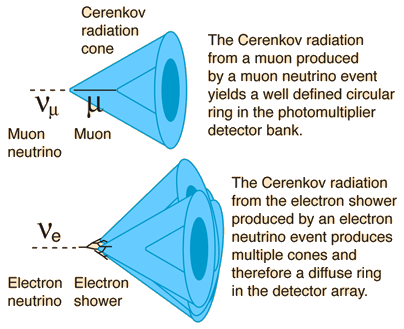 |
One of the valuable applications of Cerenkov radiation is in the detection of neutrinos and distintinguishing between different types of neutrinos.
An energetic muon remains intact while slowing down and its Cerenkov cone paints out a well-defined circular ring on the detector array. A high energy electron on the other hand will produce a diffuse ring on the detectors because it will produce a shower of electrons, each with its own Cerenkov cone.
|
Cerenkov Applications
Cerenkov radiation can be used to detect the occurrence of certain nuclear interactions. Such interactions can release large amounts of energy and eject particles at highly relativistic speeds. If these interactions take place in water or another clear substance, then the Cerenkov radiation emitted as the reaction products travel through the water can be detected by photomultiplier tubes.
This kind of detection is to be used in the Sudbury Neutrino Observatory to detect neutrino interactions. The Super-Kamiokande neutrino detector facility in Japan has 11,000 photomuliplier tubes in place to detect Cerenkov radiation and is able to detect and distinguish electron and muon neutrinos.
Measurements of particle speeds can be made by measuring the angle of the Cerenkov cone, like photographing ship wakes to measure ship speeds. A portion of the light emitted by the decelerated particle is coherent and is emitted at a characteristic angle

The total amount of energy appearing in Cerenkov radiation is small compared to the total energy loss by ionization as the particle enters the medium. According to Rohlf, a relativistic particle near the speed of light will lose energy at the rate of about 200 MeV/m, and of that loss only about 40 keV/m will be in Cerenkov radiation, about 1/5000 of the total.
Although the example given here is for electrons in water, applicable to the use of Cerenkov radiation for neutrino detection, Cerenkov radiation occurs for any charged particle which enters a material medium at a speed greater than the speed of light in that medium.
The Cerenkov radiation is independent of the mass of the particle, depending only upon its charge and speed. Cerenkov radiation is emitted at all frequencies in the visible if it occurs in an optically transparent medium, but the energy per unit wavelength is proportional to the inverse cube of the wavelength. Short wavelengths are then preferred, and the visible color is described by Evans as "bluish white".
Early Cerenkov detectors used glass, lucite and mica as detector media. They all had indices of refraction around n=1.5, so the limiting Cerenkov angle was about 48°. Although the Cerenkov radiation can be produced at all forward angles less than the limiting angle as the particle slows down, in practice the emission is seen as a narrow cone with only a few degrees width.
The particles slow down very quickly, so the radiation comes from a very short path length in the medium and a very short time interval (<10^-10 sec,Richtmyer, et al). The emission comes from discrete atoms at steps along the path, and is emitted coherently. As early as 1951, Mather reported the use of Cerenkov radiation for determining the energy of 340 MeV protons with an uncertainty of only +/- 0.8 MeV.
Analytical treatments of Cerenkov radiation were carried out by Frank & Tam and by Fermi
Cyclotron Frequency
One of the early tests of the relativistic mass expression was the behavior of cyclotrons when the speed of the accelerated particles approached the speed of light. The non-relativistic expression for the cyclotron frequency indicated that the particles could continue to be accelerated by the constant angular frequency :
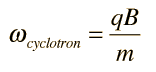
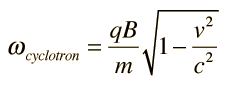
it was clear that the frequency must be changed as the particles accelerated. The success of the accelerators which used the above frequency was a test for the expression for relativistic mass.
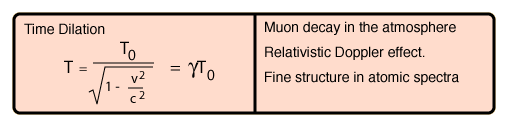
Time Dilation

 |
A clock in a moving frame will be seen to be running slow, or "dilated" according to the Lorentz transformation. The time will always be shortest as measured in its rest frame. The time measured in the frame in which the clock is at rest is called the "proper time".
|
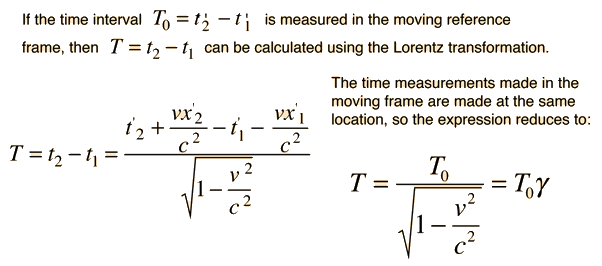
For small velocities at which the relativity factor is very close to 1, then the time dilation can be expanded in a binomial expansion to get the approximate expression:
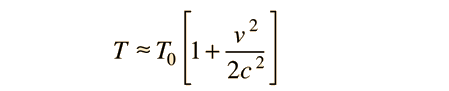
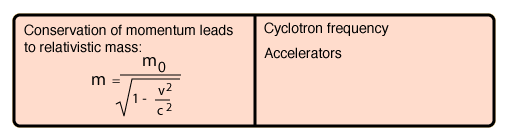
Relativistic Mass
The increase in effective mass with speed is given by the expression
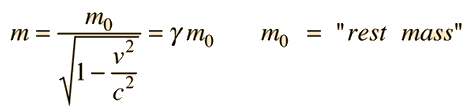
It follows from the Lorentz transformation when collisions are described from a fixed and moving reference frame, where it arises as a result of conservation of momentum.
The increase in relativistic effective mass makes the speed of light c the speed limit of the universe. This increased effective mass is evident in cyclotrons and other accelerators where the speed approaches c. Exploring the calculation above will show that you have to reach 14% of the speed of light, or about 42 million m/s before you change the mass by 1%.
Relativistic Mass Example
At the electron accelerator in Cambridge, Mass., the final acceleration stage has the following characteristics:
| Feed electrons | Electrons out | |
| Velocity | 0.99986 c | 0.999999996 c |
| Mass | 60 m0 | 11,180 m0 |
| Relative time for auto trip | 2 hr | 1 hr 59 min 59 sec |
This increase in velocity requires a 186x increase in energy, yet only saves one second off a two hour journey.
Problems with variable mass
Even though circumstances like that described at the Cambridge accelerator are conveniently described by assuming an increasing mass, that is not the only way to describe these experiments, and there are problems with the concept of variable relativistic mass. Einstein's point of view is described in the following quote:
| "It is not good to introduce the concept of the mass of a moving body for which no clear definition can be given. It is better to introduce no other mass concept than the 'rest mass' m. Instead of introducing M it is better to mention the expression for the momentum and energy of a body in motion." |  |
Upon being introduced to special relativity for the first time, it is easier to contemplate concepts like the speed of light as the speed limit of the universe by envisioning the mass as increasing to infinity at velocity c. However, when one has become familiar with the concepts of relativistic momentum and relativistic energy, there is no real need for the variable mass concept.
Relativistic Range
The ability to detect a short-lived particle depends upon it having enough range in the accelerator to reach the detector. This is a serious problem with particles which may have an average lifetime as short at 10-16 seconds! Even traveling at the speed of light, it will traveled only 0.03 micrometers before decaying, on average. The practical detection of short-lived particles depends upon relativistic time dilation.
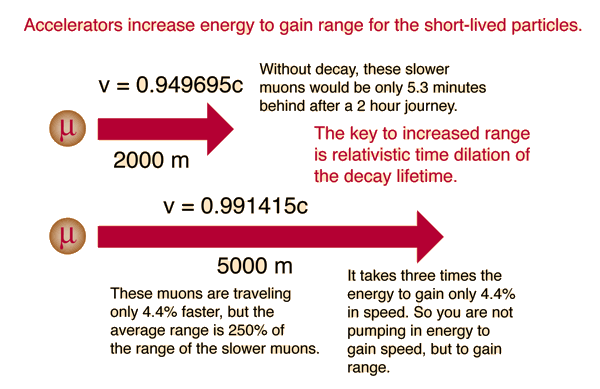
Because the clocks of the high speed particles run more slowly than the laboratory frame, the particles have a longer range in the accelerator than a non-relativistic treatment would anticipate. The numbers in the above illustration can be verified in the calculation below.
Note: Muon parameters will be entered by default. All values may be changed. An example requiring the relativistic range to explain the observed data is the muon flux at the Earth's surface.
Is time immutable?
Our common sense tells us that we have no control over time, and our cultures are full of sayings like "time marches on" which suggest that the inevitable flow of time is independent of all other aspects of our existence.
Our experience with mechanical reality reinforces the notion of time as an independent variable. For example, if we throw a ball, it follows a well-defined and deterministic trajectory determined by the acceleration of gravity and the initial conditions. Once those initial conditions are specified, the position of the ball can be calculated precisely at any time t.
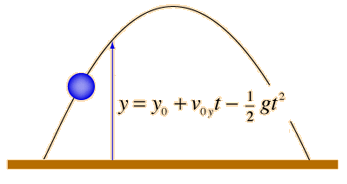 |
When we see the ball in motion, we follow it with the progress of time and clearly perceive the direction of time, but the equations themselves would work just as well with time running backward, as if we played the video of the ball toss backward. The mathematics of Newtonian mechanics does not tell us the direction of time.
|
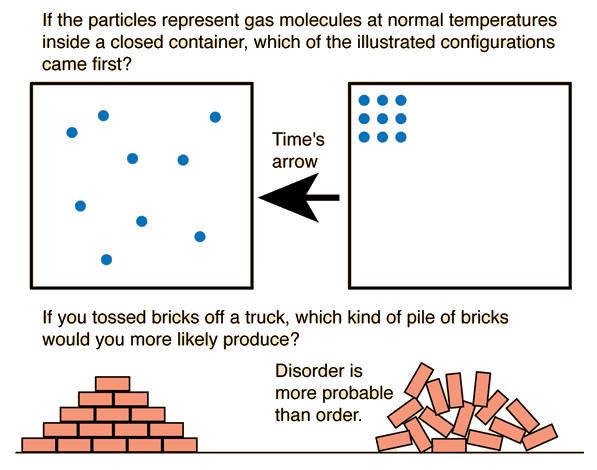
The first indication that time is not independent of everything else in the universe came with Einstein's development of the ideas of special relativity with the idea of time dilation: time progresses more slowly in a reference frame moving at high speed relative to us. Then in his development of general relativity came the additional idea that time is affected by a gravitational field and therefore proceeds more slowly in the presence of a large gravitational mass.
While the common sense picture of time as immutable applies to the vast majority of our experience, the picture that arises from relativity is that the universe is more accurately pictured as a space-time continuum where there can be mixing or transformation of the space and time coordinates.
Transforming to another space reference frame can also alter a measured time interval. This is seen clearly in the muon experiment and also experienced routinely in the range of unstable particles in accelerators.
More profound alteration of our common sense time notions occurs near a black hole where the rate of time progress approaches zero as the event horizon is approached. This can also lead to modeling of the big bang as a beginning of space and time.
Earth as a Time Data-Logger
Any repetitive process can be used as a clock, and the dependable motion of the Earth around the sun leaves a record of past time in a number of ways. The record of the seasons is kept by many living things, and we can look back 6000 years in the record of tree rings in bristle cone pine trees. Annual layering of lake sediment is recorded in lake varves. Even longer records of annual variations can be found in cores of permanent ice fields and in various kinds of sediment.
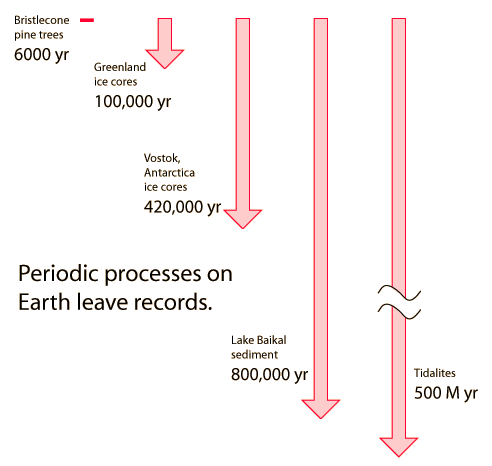
Gonzalez and Richards describe a number of interesting examples in a chapter titled "At Home on a Data-Recorder".
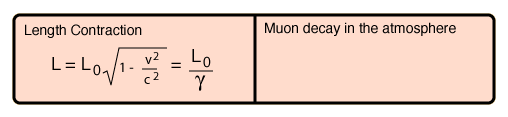
Length Contraction
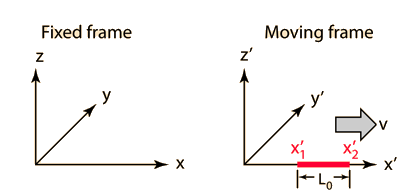 |
The length of any object in a moving frame will appear foreshortened in the direction of motion, or contracted. The amount of contraction can be calculated from the Lorentz transformation. The length is maximum in the frame in which the object is at rest.
|
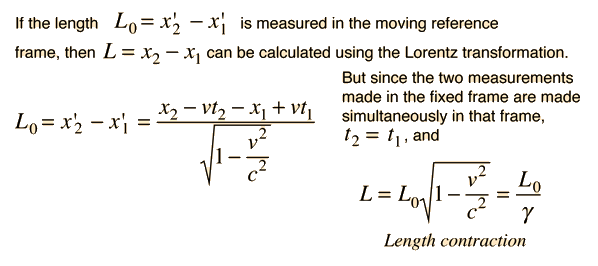
For v = c, L = L
Time Dilation

 |
A clock in a moving frame will be seen to be running slow, or "dilated" according to the Lorentz transformation. The time will always be shortest as measured in its rest frame. The time measured in the frame in which the clock is at rest is called the "proper time".
|
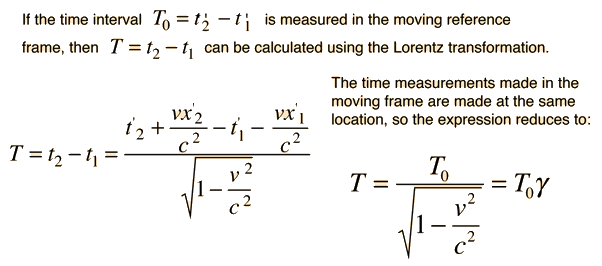
For small velocities at which the relativity factor is very close to 1, then the time dilation can be expanded in a binomial expansion to get the approximate expression:
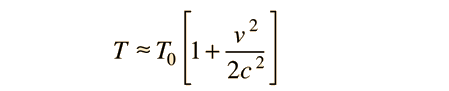
Atomic Fine Structure
One of the great successes of the quantum theory was the prediction of the energy levels of the hydrogen atom. When attempts were made to explain the fine structure of the hydrogen spectral lines, it was found that the splitting of the lines was in error by a factor of two. It was realized that relativistic time dilation must be used in calculating the frequencies, and calculations showed that this relativistic correction, called Thomas precession, was the factor of two which was needed for agreement with experiment.
Kaivola Time Dilation Experiment
A precise measurement of time dilation was made in a double-photon experiment by Kaviola et al. in 1985. An atomic beam of neon atoms at v= 0.004c was excited by two lasers which were colinear with the beam and incident upon the atoms from opposite directions. The absorption frequencies for neon are shifted by both the Doppler effect and time dilation, with the Doppler shift being much larger.
By measuring a double photon transition with the two lasers from opposite directions, the Doppler shift was canceled and the time dilation shift measured precisely . The measurement was made by measuring the beat frequency between the two tunable lasers. This experiment confirmed the expected time dilation within 4 parts in 100,000.
Relativistic Mass
The increase in effective mass with speed is given by the expression
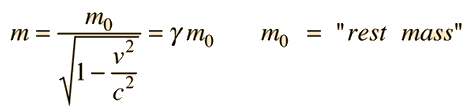
It follows from the Lorentz transformation when collisions are described from a fixed and moving reference frame, where it arises as a result of conservation of momentum.
The increase in relativistic effective mass makes the speed of light c the speed limit of the universe. This increased effective mass is evident in cyclotrons and other accelerators where the speed approaches c. Exploring the calculation above will show that you have to reach 14% of the speed of light, or about 42 million m/s before you change the mass by 1%.
Relativistic Energy
The famous Einstein relationship for energy
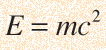
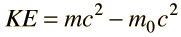
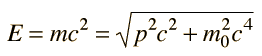 |
The relativistic energy expression is the tool used to calculate binding energies of nuclei and the energy yields of nuclear fission and fusion
Rest Mass Energy
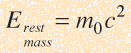
Conservation of Energy
The relativistic energy expression E = mc2 is a statement about the energy an object contains as a result of its mass and is not to be construed as an exception to the principle of conservation of energy. Energy can exist in many forms, and mass energy can be considered to be one of those forms. "Energy is the ultimate convertable currency."
(Brian Greene in The Elegant Universe).
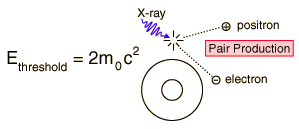
Pair Production
Every known particle has an antiparticle; if they encounter one another, they will annihilate with the production of two gamma-rays. The quantum energies of the gamma rays is equal to the sum of the mass energies of the two particles (including their kinetic energies). It is also possible for a photon to give up its quantum energy to the formation of a particle-antiparticle pair in its interaction with matter.
The rest mass energy of an electron is 0.511 MeV, so the threshold for electron-positron pair production is 1.02 MeV. For x-ray and gamma-ray energies well above 1 MeV, this pair production becomes one of the most important kinds of interactions with matter. At even higher energies, many types of particle-antiparticle pairs are produced.
Relativistic Kinetic Energy
The relativistic energy expression includes both rest mass energy and the kinetic energy of motion. The kinetic energy is then given by
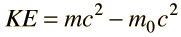
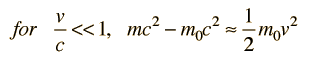 |
Kinetic Energy for v/c<<1
The relativistic kinetic energy expression can be written as
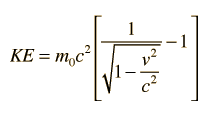
and the square root expression then expanded by use of the binomial theorem :
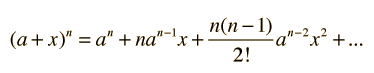
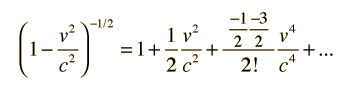
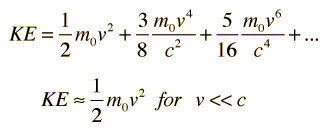
Length Contraction
 |
The length of any object in a moving frame will appear foreshortened in the direction of motion, or contracted. The amount of contraction can be calculated from the Lorentz transformation.
The length is maximum in the frame in which the object is at rest.
|
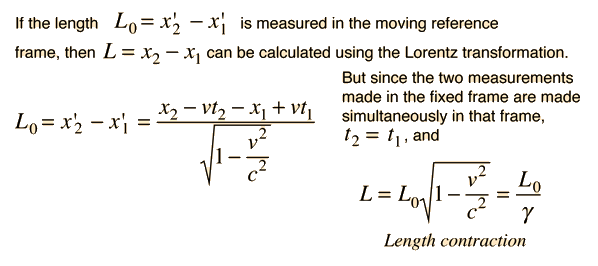
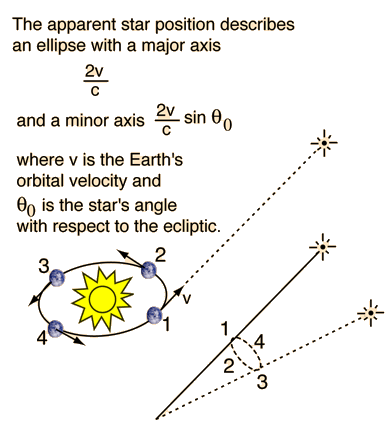
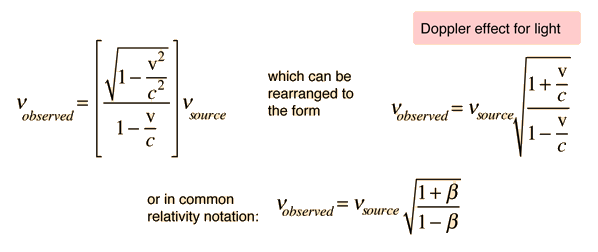
Relativistic Doppler Shift

Doppler Effect, Electromagnetic Waves
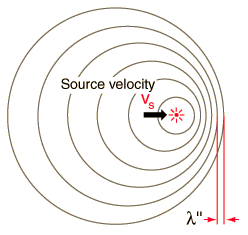 | The Doppler effect is observed with visible light and all other electromagnetic waves. Just as in the case of sound waves, the wavelength in the direction of the source motion is shortened to where all quantities here are measured in the observer's frame. To relate this to the source frequency, it must be expressed in terms of by using the time dilation expression 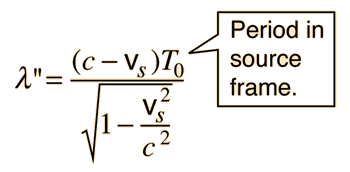 This is used to get the frequency. |
Fractional Wavelength Change
For purposes of determining recession speed of stars and galaxies with the Doppler effect by observation of the red shift of spectral lines, it is convenient to express the Doppler effect in terms of the shift in wavelength compared to the source wavelength. For these purposes it is more convenient to define a receding velocity as positive in the wavelength relationship:
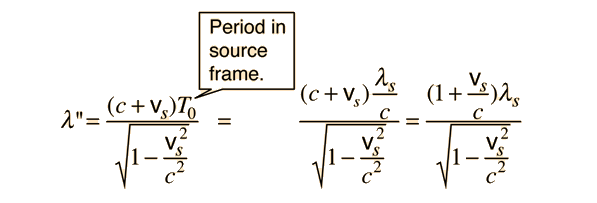
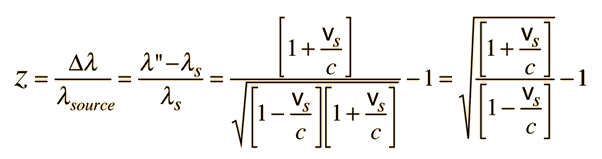
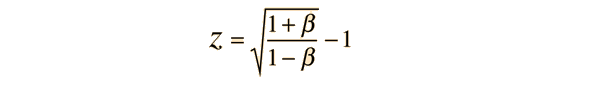
Doppler Frequency
 | From the Doppler shifted wavelength, the observed frequency is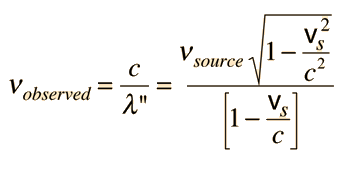  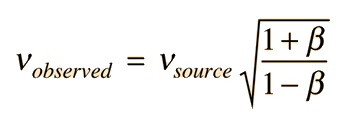 |
Galilean Transformation

Lorentz Transformation
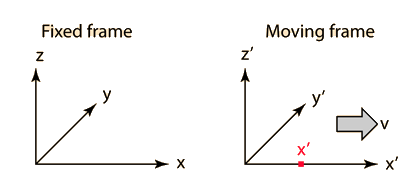 The primed frame moves with velocity v in the x direction with respect to the fixed reference frame. The reference frames coincide at t=t'=0. The point x' is moving with the primed frame. | 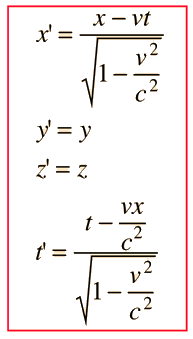 |
| The reverse transformation is: | 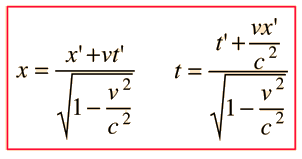 |
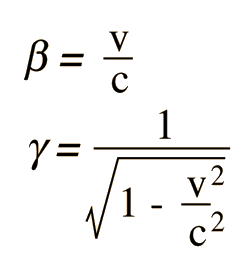 | Much of the literature of relativity uses the symbols β and γ as defined here to simplify the writing of relativistic relationships. |
Speed of Light
Experimental measurements of the speed of light have been refined in progressively more accurate experiments since the seventeenth century. Recent experiments give a speed of
but the uncertainties in this value are chiefly those of comparisons to previous standards for the length of the meter. Therefore the above speed of light has been adopted as a standard value and the length of the meter is redefined to be consistent with this value.
In vacuum, all electromagnetic waves travel at c, the speed of light
Relativity Factor
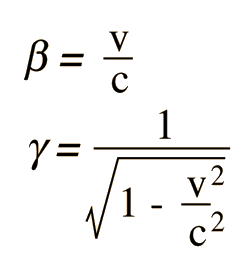 | Much of the literature of relativity uses the symbols β and γ as defined here to simplify the writing of relativistic relationships. |
For relatively low velocities where the relativity factor gamma is close to one, the binomial expansion can be used to evaluate the small relativistic corrections.
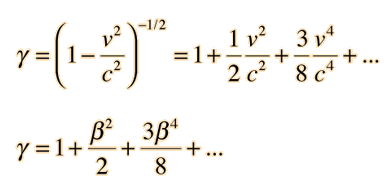
c as Speed Limit
The speed of light c is said to be the speed limit of the universe because nothing can be accelerated to the speed of light with respect to you. A common way of describing this situation is to say that as an object approaches the speed of light, its mass increases and more force must be exerted to produce a given acceleration.
There are difficulties with the "changing mass" perspective, and it is generally preferrable to say that the relativistic momentum and relativistic energy approach infinity at the speed of light. Since the net applied force is equal to the rate of change of momentum and the work done is equal to the change in energy, it would take an infinite time and an infinite amount of work to accelerate an object to the speed of light. (Sorry, Captain Kirk. We can't give you warp speed!)
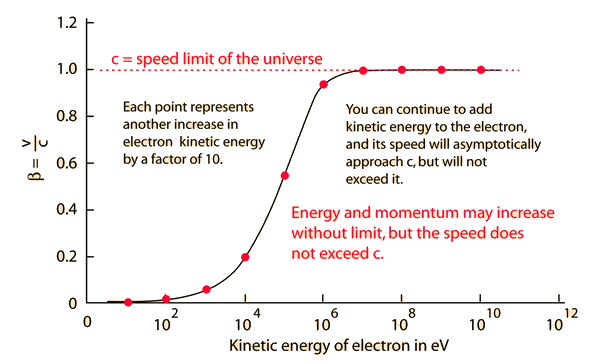
A common resistance to the speed limit is to suggest that you just accelerate two different objects to more than half of the speed of light and point them toward each other, giving a relative speed greater than c. But that doesn't work! Time and space are interwoven in such a way that no one observer ever sees another object moving toward them at greater than c.
The Einstein velocity addition deals with the transformation of velocities, always yielding a relative velocity less than c. It doesn't agree with your common sense, but it appears to be the way the universe works.
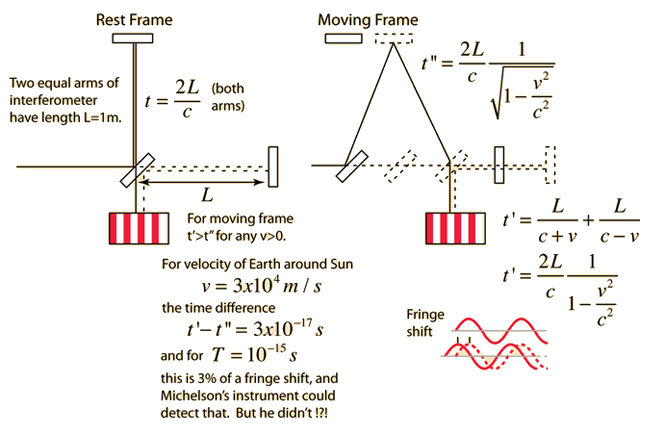
Michelson-Morley Data
Over a period of about 50 years, the Michelson-Morley experiment was repeated with growing levels of sophistication. The overall result is a high level of confidence that the wavelength shift is consistent with zero.
| L (cm) | Calculation | Observation | Ratio | |
| Michelson, 1881 | 120 | .04 | .02 | 2 |
| Michelson & Morley 1887 | 1100 | .40 | .01 | 40 |
| Morley & Miller, 1902-04 | 3220 | 1.13 | .015 | 80 |
| Illingworth, 1927 | 200 | .07 | .0004 | 175 |
| Joos,1930 | 2100 | .75 | .002 | 375 |
Double Star Images
Suppose we take the common-sense position that if a star is moving toward us, then the light from that star must have a higher velocity toward us. Since light does not depend upon the medium (space) then the light speed surely must add to the velocity of the source? From this point of view, consider the observation of a binary star system.
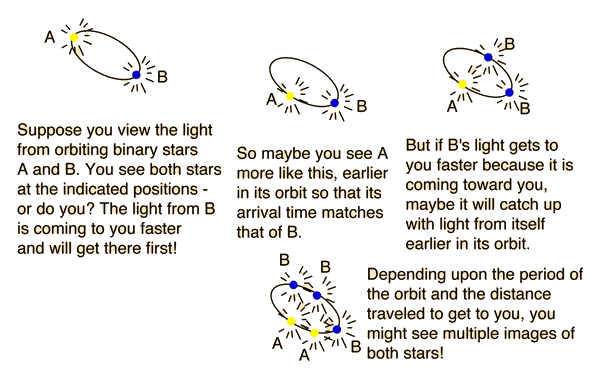
As a youthful clerk in a Swiss patent office, Einstein may have had time to reflect upon the contradictions in star images that arise if the light velocity depends upon the velocity of the star toward us.
Aberration of Starlight
You have to tilt your telescope to catch the star light just as you have to tilt your umbrella to keep off wind-driven rain. It is a matter of relative velocity.

Common experience leads you to expect that the velocity of the light relative to the Earth would be greater than the velocity of the light relative to the star. That is, you expect the velocity of the light with respect to the Earth to be the hypotenuse of the triangle and therefore greater than c. But observations are consistent with the hypotenuse of the triangle being just equal to c. Actual experiments involve measurements of the change in the apparent positions of stars at different times of the year.
Apparent Star Positions
You have to tilt your telescope to catch the star light just as you have to tilt your umbrella to keep off wind-driven rain. It is a matter of relative velocity. As the Earth moves around the Sun, the star will appear to trace out a small ellipse. The shape of the ellipse depends on the orientation of the star to the ecliptic.
 | When a distant star is viewed from the Earth at different times of the year, its apparent position will change as a result of the Earth's velocity through space. This apparent ellipse of motion of the star is called the aberration of starlight. Measurements of the size of this ellipse offer one piece of evidence that the velocity of light is independent of observer motion. This effect is independent of the parallax which permits the determination of the distance of the closest stars by triangulation. |
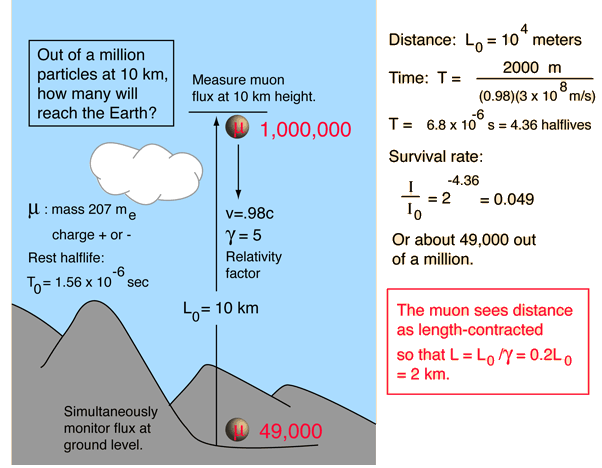
Muon Experiment
The measurement of the flux of muons at the Earth's surface produced an early dilemma because many more are detected than would be expected, based on their short half-life of 1.56 microseconds. This is a good example of the application of relativistic time dilation to explain the increased particle range for high-speed particles.
Non-Relativistic

When a distant star is viewed from the Earth at different times of the year, its apparent position will change as a result of the Earth's velocity through space. This apparent ellipse of motion of the star is called the aberration of starlight. Measurements of the size of this ellipse offer one piece of evidence that the velocity of light is independent of observer motion. This effect is independent of the parallax which permits the determination of the distance of the closest stars by triangulation. |
Muon Experiment
Relativistic, Earth-Frame Observer
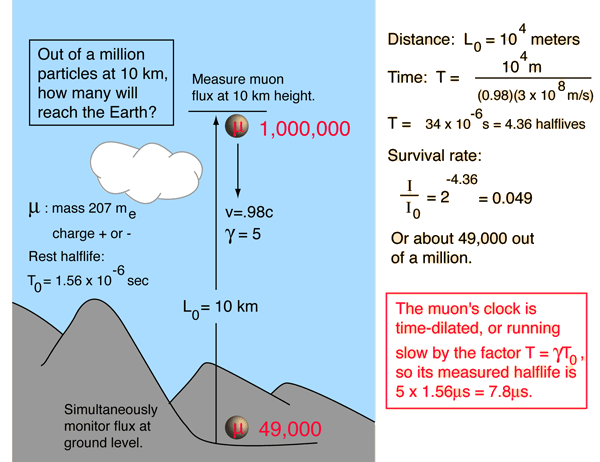
Muon Experiment
Relativistic, Muon-Frame Observer



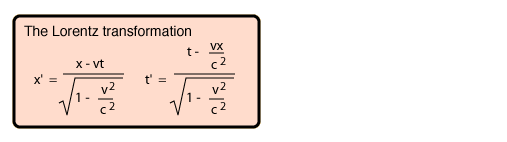






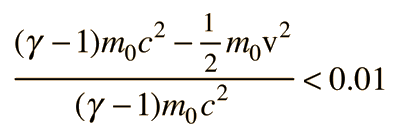
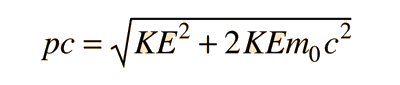
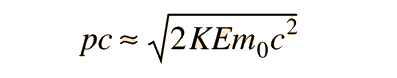
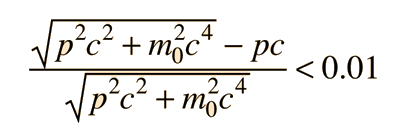


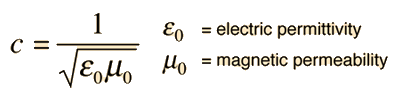
Sem comentários:
Enviar um comentário