A mecânica quântica
Nobel Prizes (10) - Albert Einstein,Werner Heisenberg, Max Planck, Louis de Broglie, Niels Bohr, Erwin Schrödinger, Max Born, Paul Dirac, Wolfgang Pauli, Richard Feynman
A mecânica quântica é a teoria física que obtém sucesso no estudo dos sistemas físicos cujas dimensões são próximas ou abaixo da escala atômica, tais como moléculas, átomos, eletrões, protões e de outras partículas subatómicas, muito embora também possa descrever fenómenos macroscópicos em diversos casos. A Mecânica Quântica é um ramo fundamental da física com vasta aplicação. A teoria quântica fornece descrições precisas para muitos fenômenos previamente inexplicados tais como a radiação de corpo negro e as órbitas estáveis do eletrão.
Apesar de na maioria dos casos a Mecânica Quântica ser relevante para descrever sistemas microscópicos, os seus efeitos específicos não são somente perceptíveis em tal escala. Por exemplo, a explicação de fenômenos macroscópicos como asuper fluidez e a supercondutividade só é possível se considerarmos que o comportamento microscópico da matéria é quântico. A quantidade característica da teoria, que determina quando ela é necessária para a descrição de um fenômeno, é a chamada constante de Planck, que tem dimensão demomento angular ou, equivalentemente, de ação.
A mecânica quântica recebe esse nome por prever um fenômeno bastante conhecido dos físicos: a quantização. No caso dos estados ligados (por exemplo, um eletrão orbitando em torno de um núcleo positivo) a Mecânica Quântica prevê que a energia (do elétrão) deve ser quantizada. Este fenômeno é completamente alheio ao que prevê a teoria clássica.
Um panorama
A palavra “quântica” (do Latim, quantum) quer dizer quantidade. Na mecânica quântica, esta palavra refere-se a uma unidade discreta que a teoria quântica atribui a certas quantidades físicas, como a energia de um eletrão contido num átomo em repouso. A descoberta de que as ondas eletromagnéticas podem ser explicadas como uma emissão de pacotes de energia (chamados quanta) conduziu ao ramo da ciência que lida com sistemas moleculares,atômicos e subatômicos. Este ramo da ciência é atualmente conhecido como mecânica quântica.
A mecânica quântica é a base teórica e experimental de vários campos da Física e da Química, incluindo a física da matéria condensada, física do estado sólido, física atômica, física molecular,química computacional, química quântica, física de partículas, e física nuclear. Os alicerces da mecânica quântica foram estabelecidos durante a primeira metade do século XX por Albert Einstein,Werner Heisenberg, Max Planck, Louis de Broglie, Niels Bohr, Erwin Schrödinger, Max Born, John von Neumann, Paul Dirac, Wolfgang Pauli, Richard Feynman e outros. Alguns aspectos fundamentais da contribuição desses autores ainda são alvo de investigação.
Normalmente é necessário utilizar a mecânica quântica para compreender o comportamento de sistemas em escala atômica ou molecular. Por exemplo, se a mecânica clássica governasse o funcionamento de um átomo, o modelo planetário do átomo – proposto pela primeira vez porRutherford – seria um modelo completamente instável. Segundo a teoria eletromagnética clássica, toda a carga elétrica acelerada emite radiação. Por outro lado, o processo de emissão de radiação consome a energia da partícula. Dessa forma, o elétron, enquanto caminha na sua órbita, perderia energia continuamente até colapsar contra o núcleo positivo!
O conceito de estado na mecânica quântica
Em física, chama-se "sistema" um fragmento concreto da realidade que foi separado para estudo. Dependendo do caso, a palavra sistema refere-se a um elétron ou um próton, um pequeno átomo de hidrogênio ou um grande átomo de urânio, uma molécula isolada ou um conjunto de moléculas interagentes formando um sólido ou um vapor. Em todos os casos, sistema é um fragmento da realidade concreta para o qual deseja-se chamar atenção.
Dependendo da partícula pode-se inverter polarizações subsequentes de aspecto neutro.
A especificação de um sistema físico não determina unicamente os valores que experimentos fornecem para as suas propriedades (ou as probabilidades de se medirem tais valores, em se tratando de teorias probabilísticas). Além disso, os sistemas físicos não são estáticos, eles evoluem com o tempo, de modo que o mesmo sistema, preparado da mesma forma, pode dar origem a resultados experimentais diferentes dependendo do tempo em que se realiza a medida (ou a histogramas diferentes, no caso de teorias probabilísticas).
Essa ideia conduz a outro conceito-chave: o conceito de "estado". Um estado é uma quantidade matemática (que varia de acordo com a teoria) que determina completamente os valores das propriedades físicas do sistema associadas a ele num dado instante de tempo (ou as probabilidades de cada um de seus valores possíveis serem medidos, quando se trata de uma teoria probabilística). Em outras palavras, todas as informações possíveis de se conhecer em um dado sistema constituem seu estado
Essa ideia conduz a outro conceito-chave: o conceito de "estado". Um estado é uma quantidade matemática (que varia de acordo com a teoria) que determina completamente os valores das propriedades físicas do sistema associadas a ele num dado instante de tempo (ou as probabilidades de cada um de seus valores possíveis serem medidos, quando se trata de uma teoria probabilística). Em outras palavras, todas as informações possíveis de se conhecer em um dado sistema constituem seu estado
Cada sistema ocupa um estado num instante no tempo e as leis da física devem ser capazes de descrever como um dado sistema parte de um estado e chega a outro. Em outras palavras, as leis da física devem dizer como o sistema evolui (de estado em estado).
Muitas variáveis que ficam bem determinadas na mecânica clássica são substituídas por distribuições de probabilidades na mecânica quântica, que é uma teoria intrinsicamente probabilística (isto é, dispõe-se apenas de probabilidades não por uma simplificação ou ignorância, mas porque isso é tudo que a teoria é capaz de fornecer).
A representação do estado
No formalismo da mecânica quântica, o estado de um sistema num dado instante de tempo pode ser representado de duas formas principais:
O estado é representado por uma função complexa das posições ou dos momenta de cada partícula que compõe o sistema. Essa representação é chamada função de onda.
Também é possível representar o estado por um vetor num espaço vetorial complexo. Esta representação do estado quântico é chamada vetor de estado. Devido à notação introduzida porPaul Dirac, tais vetores são usualmente chamados kets (sing.: ket).
Em suma, tanto as "funções de onda" quanto os "vetores de estado" (ou kets) representam os estados de um dado sistema físico de forma completa e equivalente e as leis da mecânica quântica descrevem como vetores de estado e funções de onda evoluem no tempo.
Estes objetos matemáticos abstratos (kets e funções de onda) permitem o cálculo da probabilidade de se obter resultados específicos em um experimento concreto. Por exemplo, o formalismo da mecânica quântica permite que se calcule a probabilidade de encontrar um elétron em uma região particular em torno do núcleo.
Para compreender seriamente o cálculo das probabilidades a partir da informação representada nos vetores de estado e funções de onda é preciso dominar alguns fundamentos de álgebra linear.
Formulação matemática
Muitos fenómenos quânticos difíceis de se imaginar concretamente podem ser compreendidos com um pouco de abstração matemática. Há três conceitos fundamentais da matemática - mais especificamente da álgebra linear - que são empregados constantemente pela mecânica quântica. São estes: (1) o conceito de operador; (2) de autovetor; e (3) de autovalor.
Vetores e espaços vetoriais
Na álgebra linear, um espaço vetorial (ou o espaço linear) é uma coleção dos objetos abstratos (chamados vetores) que possuem algumas propriedades que não serão completamente detalhadas aqui.
Por agora, importa saber que tais objetos (vetores) podem ser adicionados uns aos outros e multiplicados por um número escalar. O resultado dessas operações é sempre um vetor pertencente ao mesmo espaço. Os espaços vetoriais são os objetos básicos do estudo na álgebra linear, e têm várias aplicações na matemática, na ciência, e na engenharia.
O espaço vetorial mais simples e familiar é o espaço Euclidiano bidimensinal. Os vetores neste espaço são pares ordenados e são representados graficamente como "setas" dotadas de módulo, direção e sentido. No caso do espaço euclidiano bidimensional, a soma de dois vetores quaisquer pode ser realizada utilizando a regra do paralelogramo.
Todos os vetores também podem ser multiplicados por um escalar - que no espaço Euclidiano é sempre um número real. Esta multiplicação por escalar poderá alterar o módulo do vetor e seu sentido, mas preservará sua direção. O comportamento de vetores geométricos sob estas operações fornece um bom modelo intuitivo para o comportamento dos vetores em espaços mais abstratos, que não precisam de ter a mesma interpretação geométrica. Como exemplo, é possível citar o espaço de Hilbert (onde "habitam" os vetores da mecânica quântica). Sendo ele também um espaço vetorial, é certo que possui propriedades análogas àquelas do espaço Euclidiano.
Os operadores na mecânica quântica
Um operador é um ente matemático que estabelece uma relação funcional entre dois espaços vetoriais. A relação funcional que um operador estabelece pode ser chamada transformação linear. Os detalhes mais formais não serão apontados aqui. Interessa, por enquanto, desenvolver uma ideia mais intuitiva do que são esses operadores.
Por exemplo, considere o Espaço Euclidiano. Para cada vetor nesse espaço é possível executar uma rotação (de um certo ângulo) e encontrar outro vetor no mesmo espaço. Como essa rotação é uma relação funcional entre os vetores de um espaço, podemos definir um operador que realize essa transformação. Assim, dois exemplos bastante concretos de operadores são os de rotação e translação.
Do ponto de vista teórico, a semente da ruptura entre as física quântica e clássica está no emprego dos operadores. Na mecânica clássica, é usual descrever o movimento de uma partícula com uma funçãoescalar do tempo. Por exemplo, imagine que vemos um vaso de flor caindo de uma janela. Em cada instante de tempo podemos calcular a que altura se encontra o vaso. Em outras palavras, descrevemos a grandeza posição com um número (escalar) que varia em função do tempo.
Uma característica distintiva na mecânica quântica é o uso de operadores para representar grandezas físicas. Ou seja, não são somente as rotações e translações que podem ser representadas por operadores. Na mecânica quântica grandezas como posição, momento linear, momento angular e energia também são representados por operadores.
Até este ponto já é possível perceber que a mecânica quântica descreve a natureza de forma bastante abstrata. Em suma, os estados que um sistema físico pode ocupar são representados por vetores de estado (kets) ou funções de onda (que também são vetores, só que no espaço das funções). As grandezas físicas não são representadas diretamente por escalares (como 10 m, por exemplo), mas por operadores.
Para compreender como essa forma abstrata de representar a natureza fornece informações sobre experimentos reais é preciso discutir um último tópico da álgebra linear: o problema de autovalor e autovetor.
O problema de autovalor e autovetor
O problema de autovalor e autovetor é um problema matemático abstrato sem o qual não é possível compreender seriamente o significado da mecânica quântica.
Em primeiro lugar, considere o operador  de uma transformação linear arbitrária que relacione vetores de um espaço E com vetores do mesmo espaço E. Neste caso, escreve-se [eq.01]:

Observe que qualquer matriz quadrada satisfaz a condição imposta acima desde que os vetores no espaço E possam ser representados como matrizes-coluna e que a atuação de  sobre os vetores de Eocorra conforme o produto de matrizes a seguir:

Como foi dito, a equação acima ilustra muito bem a atuação de um operador do tipo definido em [eq.01]. Porém, é possível representar a mesma ideia de forma mais compacta e geral sem fazer referência à representação matricial dos operadores lineares [eq.02]:

Para cada operador  existe um conjunto  tal que cada vetor do conjunto satisfaz [eq.03]:
tal que cada vetor do conjunto satisfaz [eq.03]:
 tal que cada vetor do conjunto satisfaz [eq.03]:
tal que cada vetor do conjunto satisfaz [eq.03]:


A equação acima é chamada equação de autovalor e autovetor. Os vetores do conjunto  são chamados autovetores. Os escalares do conjunto
são chamados autovetores. Os escalares do conjunto  são chamados autovalores. O conjunto dos autovalores
são chamados autovalores. O conjunto dos autovalores  também é chamado espectro do operador Â.
também é chamado espectro do operador Â.
 são chamados autovetores. Os escalares do conjunto
são chamados autovetores. Os escalares do conjunto  são chamados autovalores. O conjunto dos autovalores
são chamados autovalores. O conjunto dos autovalores  também é chamado espectro do operador Â.
também é chamado espectro do operador Â.
Para cada autovalor corresponde um autovetor e o número de pares autovalor-autovetor é igual à dimensão do espaço E onde o operador  está definido. Em geral, o espectro de um operador Âqualquer não é contínuo, mas discreto. Encontrar os autovetores e autovalores para um dado operador é o chamado problema de autovalor e autovetor.
De antemão o problema de autovalor e autovetor possui duas características:
(1)  satisfaz o problema para qualquer operador Â. Por isso, o vetor nulo
satisfaz o problema para qualquer operador Â. Por isso, o vetor nulo  não é considerado uma resposta do problema.
não é considerado uma resposta do problema.
 satisfaz o problema para qualquer operador Â. Por isso, o vetor nulo
satisfaz o problema para qualquer operador Â. Por isso, o vetor nulo  não é considerado uma resposta do problema.
não é considerado uma resposta do problema.
(2) Se  satisfaz a equação de autovalor e autovetor, então seu múltiplo
satisfaz a equação de autovalor e autovetor, então seu múltiplo  também é uma resposta ao problema para qualquer
também é uma resposta ao problema para qualquer 
 satisfaz a equação de autovalor e autovetor, então seu múltiplo
satisfaz a equação de autovalor e autovetor, então seu múltiplo  também é uma resposta ao problema para qualquer
também é uma resposta ao problema para qualquer 
Enfim, a solução geral do problema de autovalor e autovetor é bastante simples. A saber:



Onde:

Como  não pode ser considerado uma solução do problema, é necessário que:
não pode ser considerado uma solução do problema, é necessário que:
 não pode ser considerado uma solução do problema, é necessário que:
não pode ser considerado uma solução do problema, é necessário que:
A equação acima é um polinômio de grau n. Portanto, para qualquer operador  há n quantidades escalares
há n quantidades escalares  distintas ou não tais que a equação de autovetor e autovalor é satisfeita.
distintas ou não tais que a equação de autovetor e autovalor é satisfeita.
 há n quantidades escalares
há n quantidades escalares  distintas ou não tais que a equação de autovetor e autovalor é satisfeita.
distintas ou não tais que a equação de autovetor e autovalor é satisfeita.
Os autovetores correspondentes aos autovalores  de um operador  podem ser obtidos facilmente substituindo os autovalores um a um na [eq.03].
de um operador  podem ser obtidos facilmente substituindo os autovalores um a um na [eq.03].
 de um operador  podem ser obtidos facilmente substituindo os autovalores um a um na [eq.03].
de um operador  podem ser obtidos facilmente substituindo os autovalores um a um na [eq.03].
O significado físico dos operadores, seus autovetores e autovalores
Para compreender o significado físico de toda essa representação matemática abstrata, considere o exemplo do operador de Spin na direção z: 

Na mecânica quântica, cada partícula tem associada a si uma quantidade sem análogo clássico chamada spin ou momento angular intrínseco. O spin de uma partícula é representado como um vetor com projeções nos eixos x, y e z. A cada projeção do vetor spin : corresponde um operador:
corresponde um operador:
 corresponde um operador:
corresponde um operador:
O operador  é geralmente representado da seguinte forma:
é geralmente representado da seguinte forma:
 é geralmente representado da seguinte forma:
é geralmente representado da seguinte forma:
É possível resolver o problema de autovetor e autovalor para o operador  Nesse caso obtém-se:
Nesse caso obtém-se:
 Nesse caso obtém-se:
Nesse caso obtém-se:
ou sej
portanto, os autovalores são  e
e 
 e
e 
Aspectos históricos
A história da mecânica quântica começou essencialmente em 1838 com a descoberta dos raios catódicos por Michael Faraday, a enunciação em 1859 do problema da radiação de corpo negro porGustavo Kirchhoff, a sugestão 1877 por Ludwig Boltzmann que os estados de energia de um sistema físico poderiam ser discretos, e a hipótese por Planck em 1900 de que toda a energia é irradiada e absorvida na forma de elementos discretos chamados quanta. Segundo Planck, cada um desses quanta tem energia proporcional à frequência ν da radiação eletromagnética emitida ou absorvida.

Planck insistiu que este foi apenas um aspecto dos processos de absorção e emissão de radiação e não tinha nada a ver com a realidade física da radiação em si. No entanto, naquele tempo isso parecia não explicar o efeito fotoelétrico (1839), ou seja, que a luz brilhante em certos materiais pode ejetar elétrons do material. Em 1905, baseando seu trabalho na hipótese quântica de Planck, Albert Einsteinpostulou que a própria luz é formada por quanta individuais.
Em meados da década de 1920, a evolução da mecânica quântica rapidamente fez com que ela se tornasse a formulação padrão para a física atômica. No verão de 1925, Bohr e Heisenberg publicaram resultados que fechavam a "Antiga teoria quântica". Quanta de luz vieram a ser chamados fótons(1926). Da simples postulação de Einstein nasceu uma enxurrada de debates, teorias e testes e, então, todo o campo da física quântica, levando à sua maior aceitação na quinta Conferência de Solvay em 1927.
Princípios
Primeiro princípio: Princípio da superposição
Na mecânica quântica, o estado de um sistema físico é definido pelo conjunto de todas as informações que podem ser extraídas desse sistema ao se efetuar alguma medida.
Na mecânica quântica, todos os estados são representados por vetores em um espaço vetorial complexo: o Espaço de Hilbert H. Assim, cada vetor no espaço H representa um estado que poderia ser ocupado pelo sistema. Portanto, dados dois estados quaisquer, a soma algébrica (superposição) deles também é um estado.
Como a norma dos vetores de estado não possui significado físico, todos os vetores de estado são preferencialmente normalizados. Na notação de Dirac, os vetores de estado são chamados "Kets" e são representados como aparece a seguir:

Usualmente, na matemática, são chamados funcionais todas as funções lineares que associam vetores de um espaço vetorial qualquer a um escalar. É sabido que os funcionais dos vetores de um espaço também formam um espaço, que é chamado espaço dual. Na notação de Dirac, os funcionais - elementos do Espaço Dual - são chamados "Bras" e são representados como aparece a seguir:

Segundo princípio: Medida de grandezas físicas
a) Para toda grandeza física A é associado um operador linear auto-adjunto  pertencente a A:  é o observável (autovalor do operador) representando a grandeza A.
b) Seja  o estado no qual o sistema se encontra no momento onde efetuamos a medida deA. Qualquer que seja
o estado no qual o sistema se encontra no momento onde efetuamos a medida deA. Qualquer que seja  os únicos resultados possíveis são os autovalores de
os únicos resultados possíveis são os autovalores de  do observável Â.
do observável Â.
 o estado no qual o sistema se encontra no momento onde efetuamos a medida deA. Qualquer que seja
o estado no qual o sistema se encontra no momento onde efetuamos a medida deA. Qualquer que seja  os únicos resultados possíveis são os autovalores de
os únicos resultados possíveis são os autovalores de  do observável Â.
do observável Â.
c) Sendo  o projetor sobre o subespaço associado ao valor próprio
o projetor sobre o subespaço associado ao valor próprio  a probablidade de encontrar o valor
a probablidade de encontrar o valor  em uma medida de A é:
em uma medida de A é:
 o projetor sobre o subespaço associado ao valor próprio
o projetor sobre o subespaço associado ao valor próprio  a probablidade de encontrar o valor
a probablidade de encontrar o valor  em uma medida de A é:
em uma medida de A é:  onde
onde 
d) Imediatamente após uma medida de A, que resultou no valor  o novo estado
o novo estado  do sistema é
do sistema é
 o novo estado
o novo estado  do sistema é
do sistema é 
Terceiro princípio: Evolução do sistema
Seja  o estado de um sistema ao instante t. Se o sistema não é submetido a nenhuma observação, sua evolução, ao longo do tempo, é regida pela equação de Schrödinger:
o estado de um sistema ao instante t. Se o sistema não é submetido a nenhuma observação, sua evolução, ao longo do tempo, é regida pela equação de Schrödinger:
 o estado de um sistema ao instante t. Se o sistema não é submetido a nenhuma observação, sua evolução, ao longo do tempo, é regida pela equação de Schrödinger:
o estado de um sistema ao instante t. Se o sistema não é submetido a nenhuma observação, sua evolução, ao longo do tempo, é regida pela equação de Schrödinger:
onde  é o hamiltoniano do sistema.
é o hamiltoniano do sistema.
 é o hamiltoniano do sistema.
é o hamiltoniano do sistema.
Conclusões
As conclusões mais importantes são:
Em estados ligados, como o elétron girando ao redor do núcleo de um átomo, a energia não se troca de modo contínuo, mas sim de modo discreto (descontínuo), em transições cujas energias podem ou não ser iguais umas às outras. A ideia de que estados ligados têm níveis de energias discretas é devida a Max Planck.
O fato de ser impossível atribuir ao mesmo tempo uma posição e um momento exatas a uma partícula, renunciando-se assim ao conceito de trajetória, vital em Mecânica Clássica. Em vez de trajetória, o movimento de partículas em Mecânica Quântica é descrito por meio de uma função de onda, que é uma função da posição da partícula e do tempo.
A função de onda é interpretada por Max Born como uma medida da probabilidade de se encontrar a partícula em determinada posição e em determinado tempo. Esta interpretação é a mais aceita pelos físicos hoje, no conjunto de atribuições da Mecânica Quântica regulamentados pela Escola de Copenhagen. Para descrever a dinâmica de um sistema quântico deve-se, portanto, achar sua função de onda, e para este efeito usam-se as equações de movimento, propostas por Werner Heisenberg e Erwin Schrödinger independentemente.
A função de onda é interpretada por Max Born como uma medida da probabilidade de se encontrar a partícula em determinada posição e em determinado tempo. Esta interpretação é a mais aceita pelos físicos hoje, no conjunto de atribuições da Mecânica Quântica regulamentados pela Escola de Copenhagen. Para descrever a dinâmica de um sistema quântico deve-se, portanto, achar sua função de onda, e para este efeito usam-se as equações de movimento, propostas por Werner Heisenberg e Erwin Schrödinger independentemente.
Apesar de ter sua estrutura formal basicamente pronta desde a década de 1930, a interpretação da Mecânica Quântica foi objeto de estudos por várias décadas. O principal é o problema da medição em Mecânica Quântica e sua relação com a não-localidade e causalidade. Já em 1935, Einstein, Podolski e Rosen publicaram seu Gedankenexperiment, mostrando uma aparente contradição entre localidade e o processo de Medida em Mecânica Quântica.
Nos anos 60 J. S. Bell publicou uma série de relações que seriam respeitadas caso a localidade — ou pelo menos como a entendemos classicamente — ainda persistisse em sistemas quânticos. Tais condições são chamadas desigualdades de Bell e foram testadas experimentalmente por Alain Aspect, P. Grangier, Jean Dalibard em favor da Mecânica Quântica. Como seria de se esperar, tal interpretação ainda causa desconforto entre vários físicos, mas a grande parte da comunidade aceita que estados correlacionados podem violar causalidade desta forma.
Nos anos 60 J. S. Bell publicou uma série de relações que seriam respeitadas caso a localidade — ou pelo menos como a entendemos classicamente — ainda persistisse em sistemas quânticos. Tais condições são chamadas desigualdades de Bell e foram testadas experimentalmente por Alain Aspect, P. Grangier, Jean Dalibard em favor da Mecânica Quântica. Como seria de se esperar, tal interpretação ainda causa desconforto entre vários físicos, mas a grande parte da comunidade aceita que estados correlacionados podem violar causalidade desta forma.
Tal revisão radical do nosso conceito de realidade foi fundamentada em explicações teóricas brilhantes para resultados experimentais que não podiam ser descritos pela teoria clássica, e que incluem:
Espectro de Radiação do Corpo negro, resolvido por Max Planck com a proposição da quantização da energia. Explicação do experimento da dupla fenda, no qual eléctrons produzem um padrão de interferência condizente com o comportamento ondular.
Explicação por Albert Einstein do efeito fotoelétrico descoberto por Heinrich Hertz, onde propõe que a luz também se propaga em quanta (pacotes de energia definida), os chamados fótons. O Efeito Compton, no qual se propõe que os fótons podem se comportar como partículas, quando sua energia for grande o bastante.
A questão do calor específico de sólidos sob baixas temperaturas, cuja discrepância foi explicada pelas teorias de Einstein e de Debye, baseadas na equipartição de energia segundo a interpretação quantizada de Planck. A absorção ressonante e discreta de energia por gases, provada no experimento de Franck-Hertzquando submetidos a certos valores de diferença de potencial elétrico.
A explicação da estabilidade atômica e da natureza discreta das raias espectrais, graças ao modelo do átomo de Bohr, que postulava a quantização dos níveis de energia do átomo.
O desenvolvimento formal da teoria foi obra de esforços conjuntos de muitos físicos e matemáticos da época como Erwin Schrödinger, Werner Heisenberg, Einstein, P.A.M. Dirac, Niels Bohr e John von Neumann, entre outros (de uma longa lista).
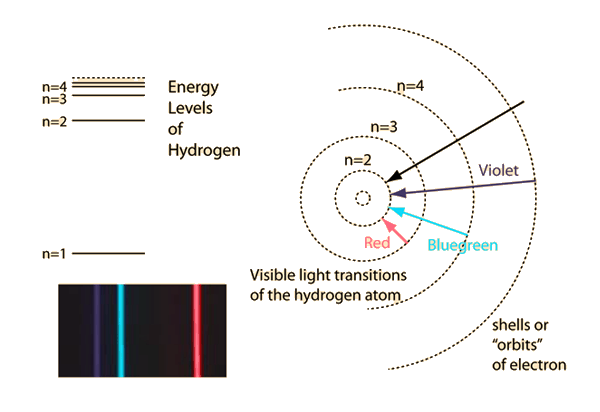
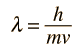
and the standing wave condition that circumference = whole number of wavelengths. In the hydrogenic case, the number n is the principal quantum number.
Quantized Energy States
The electrons in free atoms can will be found in only certain discrete energy states. These sharp energy states are associated with the orbits or shells of electrons in an atom, e.g., a hydrogen atom. One of the implications of these quantized energy states is that only certain photon energies are allowed when electrons jump down from higher levels to lower levels, producing thehydrogen spectrum. The Bohr model successfully predicted the energies for the hydrogen atom, but had significant failures that were corrected by solving the Schrodinger equation for the hydrogen atom.

Angular Momentum Quantization
In the Bohr model, the wavelength associated with the electron is given by the DeBroglie relationship
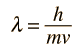
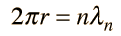
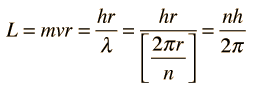 | Use in Bohr orbit |
Classical Electron Orbit
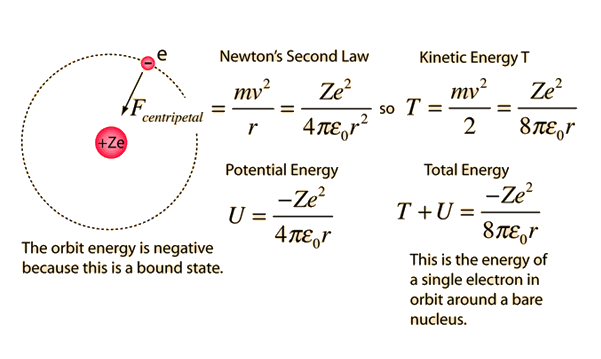
In t he Bohr theory, this classical result was combined with the quantization of angular momentum to get an expression for quantized energy levels.
Bohr Orbit
Combining the energy of the classical electron orbit with the quantization of angular momentum, the Bohr approach yields expressions for the electron orbit radii and energies:
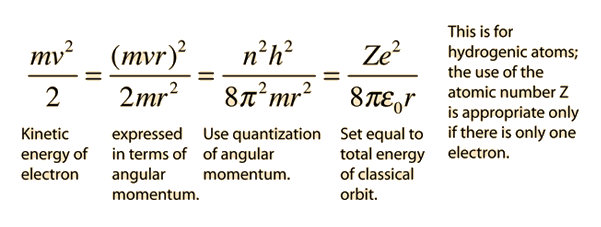
Substitution for r gives the Bohr energies and radii:
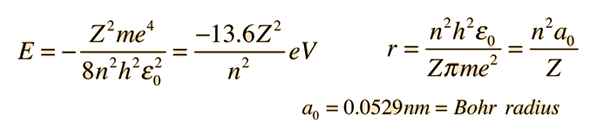
Wavelengths for Different States
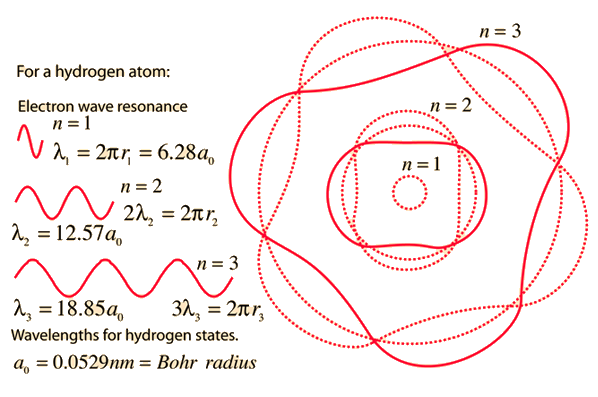
Failures of the Bohr Model
While the Bohr model was a major step toward understanding the quantum theory of the atom, it is not in fact a correct description of the nature of electron orbits. Some of the shortcomings of the model are:
1. It fails to provide any understanding of why certain spectral lines are brighter than others. There is no mechanism for the calculation of transition probabilities.
2. The Bohr model treats the electron as if it were a miniature planet, with definite radius and momentum. This is in direct violation of the uncertainty principle which dictates that position and momentum cannot be simultaneously determined.
The Bohr model gives us a basic conceptual model of electrons orbits and energies. The precise details of spectra and charge distribution must be left to quantum mechanical calculations, as with the Schrodinger equation.
One of the prominent failures of the Bohr model for atomic spectra was that it couldn't predict that one spectral line would be brighter than another. From the quantum theory came an explanation in terms of wavefunctions, and for situations where the transition probability is constant in time, it is usually expressed in a relationship called Fermi's golden rule.
In general conceptual terms, a transition rate depends upon the strength of the coupling between the initial and final state of a system and upon the number of ways the transition can happen (i.e., the density of the final states). In many physical situations the transition probability is of the form
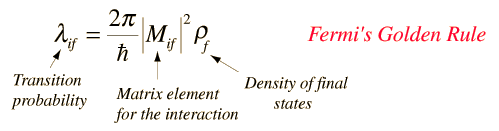
The transition probability l is also called the decay probability and is related to the mean lifetime t of the state by l = 1/t. The general form of Fermi's golden rule can apply to atomic transitions, nuclear decay, scattering ... a large variety of physical transitions.
A transition will proceed more rapidly if the coupling between the initial and final states is stronger. This coupling term is traditionally called the "matrix element" for the transition: this term comes from an alternative formulation of quantum mechanics in terms of matrices rather than the differential equations of the Schrodinger approach.
The matrix element can be placed in the form of an integral where the interaction which causes the transition is expressed as a potential V which operates on the initial state wavefunction. The transition probability is proportional to the square of the integral of this interaction over all of the space appropriate to the problem.
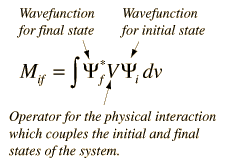
This kind of integral approach using the wavefunctions is of the same general form as that used to find the "expectation value" or expected average value of any physical variable in quantum mechanics. But in the case of an expectation value for a property like the system energy, the integral has the wavefunction representing the eigenstate of the system in both places in the integral.
The transition probability is also proportional to the density of final states rf. It is reasonably common for the final state to be composed of several states with the same energy - such states are said to be "degenerate" states. This degeneracy is sometimes expressed as a "statistical weight" which will appear as a factor in the transition probability. In many cases there will be a continuum of final states, so that this density of final states is expressed as a function of energy.
Schrodinger Equation
The Schrodinger equation plays the role of Newton's laws and conservation of energy in classical mechanics - i.e., it predicts the future behavior of a dynamic system. It is a wave equation in terms of the wavefunction which predicts analytically and precisely the probability of events or outcome. The detailed outcome is not strictly determined, but given a large number of events, the Schrodinger equation will predict the distribution of results.
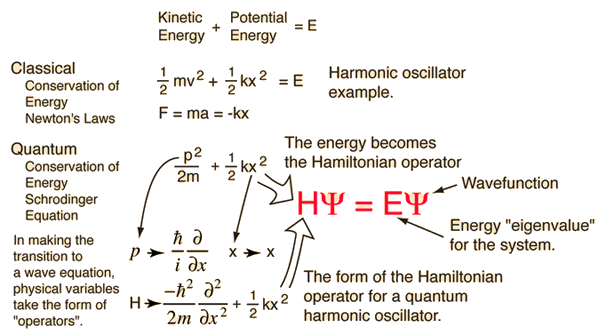
The kinetic and potential energies are transformed into the Hamiltonian which acts upon the wavefunction to generate the evolution of the wavefunction in time and space. The Schrodinger equation gives the quantized energies of the system and gives the form of the wavefunction so that other properties may be calculated.
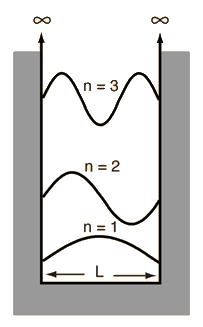
Particle in a Box
 |
The idealized situation of a particle in a box with infinitely high walls is an application of theSchrodinger equation which yields some insights into particle confinement. The wavefunction must be zero at the walls and the solution for the wavefunction yields just sine waves.
The longest wavelength is
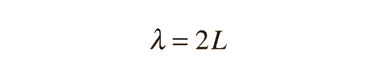 and the higher modes have wavelengths given by 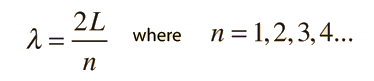 When this is substituted into the De Broglie relationship it yields momentum  |
Particle in a Box
 | When the momentum expression for the particle in a box : is used to calculate the energy associated with the particle 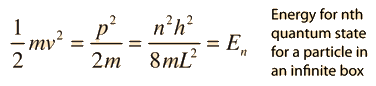 Though oversimplified, this indicates some important things about bound states for particles: 1. The energies are quantized and can be characterized by a quantum number n 2. The energy cannot be exactly zero. 3. The smaller the confinement, the larger the energy required. If a particle is confined into a rectangular volume, the same kind of process can be applied to a three-dimensional "particle in a box", and the same kind of energy contribution is made from each dimension. The energies for a three-dimensional box are  |
Particle in a Box Calculation
For a one-dimensional particle in a box , the particle energy for a box of dimension can be calculated below. For a three-dimensional box there will be three values for the quantum number n. The energies for each dimension could be calculated and added. The implication of that addition is that it takes more energy to confine a particle in three dimensions than in one, and that the minimum confinement energy for a 3D box of dimension L is three times that of a 1D box.
The Uncertainty Principle
The position and momentum of a particle cannot be simultaneously measured with arbitrarily high precision. There is a minimum for the product of the uncertainties of these two measurements. There is likewise a minimum for the product of the uncertainties of the energy and time.
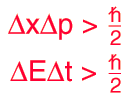
This is not a statement about the inaccuracy of measurement instruments, nor a reflection on the quality of experimental methods; it arises from the wave properties inherent in the quantum mechanical description of nature. Even with perfect instruments and technique, the uncertainty is inherent in the nature of things.
Uncertainty Principle
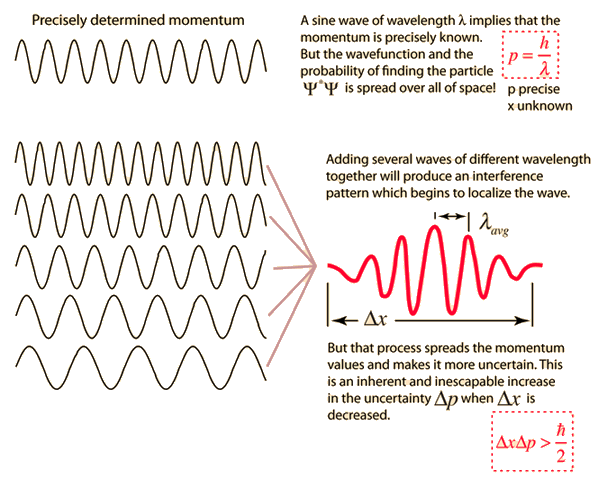
Important steps on the way to understanding the uncertainty principle are wave-particle duality and the DeBroglie hypothesis. As you proceed downward in size to atomic dimensions, it is no longer valid to consider a particle like a hard sphere, because the smaller the dimension, the more wave-like it becomes. It no longer makes sense to say that you have precisely determined both the position and momentum of such a particle.
When you say that the electron acts as a wave, then the wave is the quantum mechanical wavefunction and it is therefore related to the probability of finding the electron at any point in space. A perfect sinewave for the electron wave spreads that probability throughout all of space, and the "position" of the electron is completely uncertain.

Particle Confinement
The uncertainty principle contains implications about the energy that would be required to contain a particle within a given volume. The energy required to contain particles comes from the fundamental forces, and in particular the electromagnetic force provides the attraction necessary to contain electrons within the atom, and the strong nuclear force provides the attraction necessary to contain particles within the nucleus.
But Planck's constant, appearing in the uncertainty principle, determines the size of the confinement that can be produced by these forces. Another way of saying it is that the strengths of the nuclear and electromagnetic forces along with the constraint embodied in the value of Planck's constant determine the scales of the atom and the nucleus.
The following very approximate calculation serves to give an order of magnitude for the energies required to contain particles.

Confinement Calculation

If you examine this calculation in detail, you will note that a gross approximation was made in the relationship Δp = h/Δx. This was done to get a qualitative relationship that shows the role of Planck's constant in the relationship between Δx and Δp and thus the role of h in determining the energy of confinement.
The other reason for doing it was to get an electron confinement energy close to what is observed in nature for comparison with the energy for confining an electron in the nucleus. If you actually use the limiting case allowed by the uncertainty principle, Δp = hbar/2Δx, the confinement energy you get for the electron in the atom is only 0.06 eV.
This is because this approach only confines the electron in one dimension, leaving it unconfined in the other directions. For a more realistic atom you would need to confine it in the other directions as well. A better approximation can be obtained from the three-dimensional particle-in-a-box approach, but to precisely calculate the confinement energy requires the Shrodinger equation (see hydrogen atom calculation).
Wavefunction Contexts
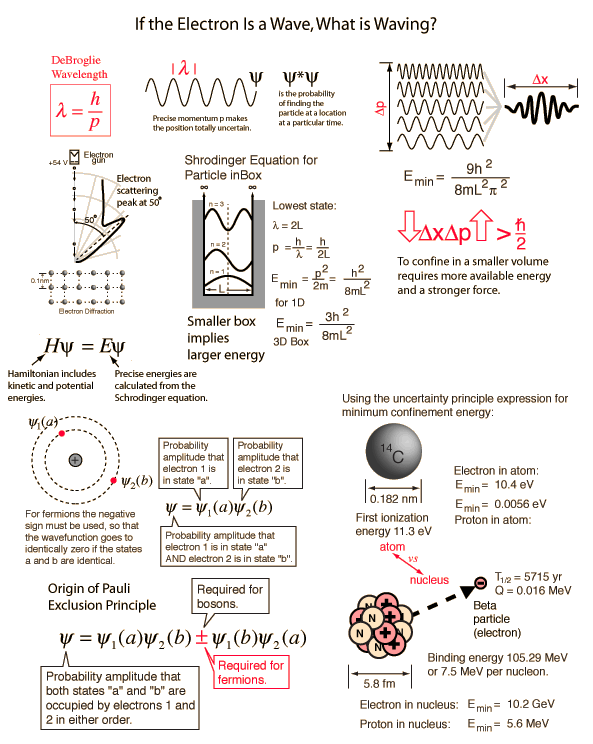
Energies in Electron Volts
Room temperature thermal energy of a molecule..................................0.04 eV
Visible light photons...........................................................................1.5-3.5 eVEnergy for the dissociation of an NaCl molecule into Na+ and Cl-ions:.............................................................................................4.2 eV
Ionization energy of atomic hydrogen ...................................................13.6 eV
Approximate energy of an electron striking a color television screen (CRT display) ...............................................................................20,000 eV
High energy diagnostic medical x-ray photons..................200,000 eV (=0.2 MeV)
Typical energies from nuclear decay:
(1) gamma..................................................................................0-3 MeV
(2) beta.......................................................................................0-3 MeV
(3) alpha......................................................................................2-10 MeV
Cosmic ray energies ...........................................................1 MeV - 1000 TeV
Electron Volts
A convenient energy unit, particularly for atomic and nuclear processes, is the energy given to an electron by accelerating it through 1 volt of electric potential difference. If an electron starts from rest at the negative plate, then the electric field will do work eV on it, giving it that amount of kinetic energy when it strikes the positive plate. The work done on the charge is given by the charge times the voltage difference, which in this case is:
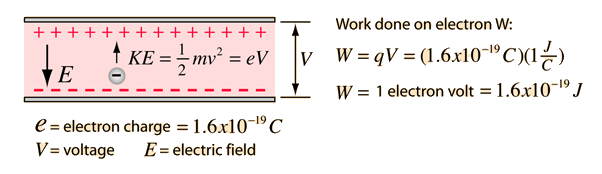
The abbreviation for electron volt is eV.

Sem comentários:
Enviar um comentário