REDSHIFT
In physics, redshift happens when light or other electromagnetic radiation from an object moving away from the observer is increased in wavelength, or shifted to the red end of the spectrum. In general, whether or not the radiation is within the visible spectrum, "redder" means an increase in wavelength – equivalent to a lower frequency and a lower photon energy, in accordance with, respectively, the wave and quantum theories of light.
Redshifts are an example of the Doppler effect, familiar in the change in the apparent pitches of sirens and frequency of the sound waves emitted by speeding vehicles. A redshift occurs whenever a light source moves away from an observer. Cosmological redshift is seen due to the expansion of the universe, and sufficiently distant light sources (generally more than a few million light years away) show redshift corresponding to the rate of increase in their distance from Earth.
Finally, gravitational redshifts are a relativistic effect observed in electromagnetic radiation moving out of gravitational fields. Conversely, a decrease in wavelength is called blueshift and is generally seen when a light-emitting object moves toward an observer or when electromagnetic radiation moves into a gravitational field.
Finally, gravitational redshifts are a relativistic effect observed in electromagnetic radiation moving out of gravitational fields. Conversely, a decrease in wavelength is called blueshift and is generally seen when a light-emitting object moves toward an observer or when electromagnetic radiation moves into a gravitational field.
Although observing redshifts and blueshifts have several terrestrial applications (such as Doppler radar and radar guns), redshifts are most famously seen in the spectroscopic observations of astronomical objects.
A special relativistic redshift formula (and its classical approximation) can be used to calculate the redshift of a nearby object when spacetime is flat. However, many cases such as black holes and Big Bang cosmology require that redshifts be calculated using general relativity.
Special relativistic, gravitational, and cosmological redshifts can be understood under the umbrella of frame transformation laws. There exist other physical processes that can lead to a shift in the frequency of electromagnetic radiation, including scattering and optical effects; however, the resulting changes are distinguishable from true redshift and not generally referred to as such (see section on physical optics and radiative transfer).
Redshift (and blueshift) may be characterized by the relative difference between the observed and emitted wavelengths (or frequency) of an object. In astronomy, it is customary to refer to this change using a dimensionless quantity called z. If λ represents wavelength and f represents frequency (note, λf = c where c is the speed of light), then z is defined by the equations:
| Based on wavelength | Based on frequency |
|---|---|
 |  |
 | 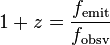 |
After z is measured, the distinction between redshift and blueshift is simply a matter of whether z is positive or negative. See the formula section below for some basic interpretations that follow when either a redshift or blueshift is observed.
For example, Doppler effect blueshifts (z < 0) are associated with objects approaching (moving closer to) the observer with the light shifting to greater energies. Conversely, Doppler effect redshifts (z > 0) are associated with objects receding (moving away) from the observer with the light shifting to lower energies. Likewise, gravitational blueshifts are associated with light emitted from a source residing within a weaker gravitational field as observed from within a stronger gravitational field, while gravitational redshifting implies the opposite conditions.
Redshift formulae
In general relativity one can derive several important special-case formulae for redshift in certain special spacetime geometries, as summarized in the following table. In all cases the magnitude of the shift (the value of z) is independent of the wavelength.[2]
| Redshift type | Geometry | Formula[22] |
|---|---|---|
| Relativistic Doppler | Minkowski space (flat spacetime) | 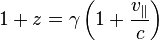  for small for small  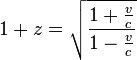 for motion completely in the radial direction. for motion completely in the radial direction. for motion completely in the transverse direction. for motion completely in the transverse direction. |
| Cosmological redshift | FLRW spacetime (expanding Big Bang universe) | 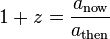 |
| Gravitational redshift | any stationary spacetime (e.g. the Schwarzschild geometry) |  (for the Schwarzschild geometry,  |
Fizeau experiment
The Fizeau experiment was carried out by Hippolyte Fizeau in 1851 to measure the relative speeds of light in moving water. Fizeau used a special interferometer arrangement to measure the effect of movement of a medium upon the speed of light.
According to the theories prevailing at the time, light traveling through a moving medium would be dragged along by the medium, so that the measured speed of the light would be a simple sum of its speed throughthe medium plus the speed of the medium. Fizeau indeed detected a dragging effect, but the magnitude of the effect that he observed was far lower than expected. His results seemingly supported the partial aether-drag hypothesis of Fresnel, a situation that was disconcerting to most physicists. Over half a century passed before a satisfactory explanation of Fizeau's unexpected measurement was developed with the advent of Albert Einstein's theory of special relativity. Einstein later pointed out the importance of the experiment for special relativity.
Although it is referred to as the Fizeau experiment, Fizeau was an active experimenter who carried out a wide variety of different experiments involving measuring the speed of light in different situations.
Experimental setup
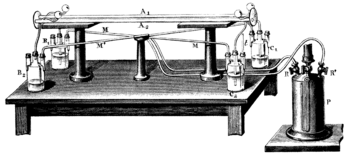
Setup of the Fizeau Experiment (1851).
A light ray emanating from the source S' is reflected by a beam splitter G and is collimated into a parallel beam by lens L. After passing the slits O1 and O2, two rays of light travel through the tubes A1 and A2, through which water is streaming back and forth as shown by the arrows. The rays reflect off a mirror m at the focus of lens L', so that one ray always propagates in the same direction as the water stream, and the other ray opposite to the direction of the water stream.
After passing back and forth through the tubes, both rays unite at S, where they produce interference fringes that can be visualized through the illustrated eyepiece. The interference pattern can be analyzed to determine the speed of light traveling along each leg of the tube.
Hoek experiment
An indirect confirmation of Fresnel's dragging coefficient was provided by Martin Hoek (1868). His apparatus was similar to Fizeau's, though in his version only one arm contained an area filled with resting water, while the other arm was in the air. As seen by an observer resting in the aether, Earth and hence the water is in motion. So the following travel times of two light rays traveling in opposite direction were calculated by Hoek (neglecting the transverse direction, see image):
  |
The travel times are not the same, which should be indicated by an interference shift. However, if Fresnel's dragging coefficient is applied to the water in the aether frame, the travel time difference (to first order in v/c) vanishes. Using different setups Hoek actually obtained a null result, confirming Fresnel's dragging coefficient. (For a similar experiment refuting the possibility of shielding the aether wind, see Hammar experiment).
In the particular version of the experiment shown here, Hoek used a prism P to disperse light from a slit into a spectrum which passed through a collimator C before entering the apparatus. With the apparatus oriented parallel to the hypothetical aether wind, Hoek expected the light in one circuit to be retarded 7/600 mm with respect to the other. Where this retardation represented an integral number of wavelengths, he expected to see constructive interference; where this retardation represented a half-integral number of wavelengths, he expected to see destructive interference. In the absence of dragging, his expectation was for the observed spectrum to be continuous with the apparatus oriented transversely to the aether wind, and to be banded with the apparatus oriented parallel to the aether wind. His actual experimental results were completely negative.
Derivation in special relativity
Einstein showed how Lorentz's equations could be derived as the logical outcome of a set of two simple starting postulates. In addition Einstein recognized that the stationary aether concept has no place in special relativity, and that the Lorentz transformation concerns the nature of space and time. Together with the moving magnet and conductor problem, the negative aether drift experiments, and the aberration of light, the Fizeau experiment was one of the key experimental results that shaped Einstein's thinking about relativity.Robert S. Shankland reported some conversations with Einstein, in which Einstein emphasized the importance of the Fizeau experiment:
He continued to say the experimental results which had influenced him most were the observations of stellar aberration and Fizeau’s measurements on the speed of light in moving water. “They were enough,” he said.
Max von Laue (1907) demonstrated that the Fresnel drag coefficient can be easily explained as a natural consequence of the relativistic formula for addition of velocities, namely:The speed of light in immobile water is c/n.From the velocity composition law it follows that the speed of light observed in the laboratory, where water is flowing with speed v (in the same direction as light) is
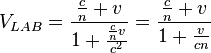
Thus the difference in speed is (assuming v is small comparing to c, approximating to the first non-trivial correction
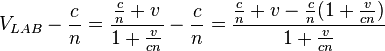
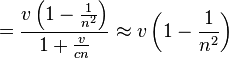
This is accurate when v/c << 1, and agrees with the formula based upon Fizeau's measurements, which satisfied the conditionv/c << 1.
Fizeau's experiment is hence supporting evidence for the collinear case of Einstein's velocity addition formula.





Sem comentários:
Enviar um comentário