Nuclear Reactions
Many kinds of nuclear reactions occur in response to the absorption of particles such as neutrons or protons. Other types of reactions may involve the absorption of gamma rays or the scattering of gamma rays. Of particular note is the resonant absorption of gamma rays in the Mossbauer effect. Specific nuclear reactions can be written down in a manner similar to chemical reaction equations. If a target nucleus X is bombarded by a particle a and results in a nucleus Y with emitted particle b, this is commonly written in one of two ways.
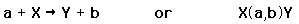
We can characterize the energetics of the reaction with a reaction energy Q, defined as the energy released in the reaction. The Q is positive if the total mass of the products is less than that of the projectile and target, indicating that the total nuclear binding energy has increased. The probability of a given type of nuclear reaction taking place is often stated as a "cross section".
Some Nuclear Reactions
* The nuclear reaction in the atmosphere which produces carbon-14 forradiocarbon dating.
Nuclear Cross Section
To characterize the probability that a certain nuclear reaction will take place, it is customary to define an effective size of the nucleus for that reaction, called a cross section. The cross section is defined by
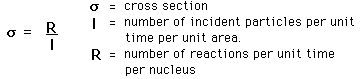
The cross section has the units of area and is on the order of the square of the nuclear radius. A commonly used unit is the barn:
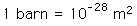
A standard old story was that in the early days of the field, a particular cross section turned out to be much bigger than expected. An experimenter exclaimed "Why, that's as big as a barn!" and a unit name was born.
Nuclear Binding Energy
Nuclei are made up of protons and neutron, but the mass of a nucleus is always less than the sum of the individual masses of the protons and neutrons which constitute it. The difference is a measure of the nuclear binding energy which holds the nucleus together. This binding energy can be calculated from the Einstein relationship:
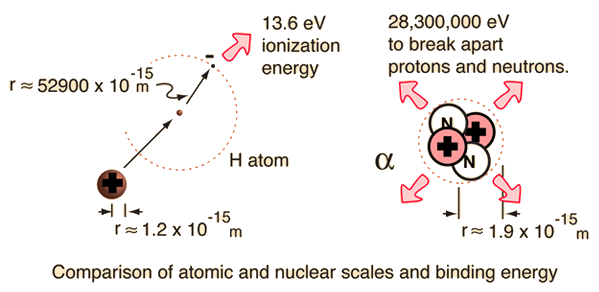
For the alpha particle Δm= 0.0304 u which gives a binding energy of 28.3 MeV.
The enormity of the nuclear binding energy can perhaps be better appreciated by comparing it to the binding energy of an electron in an atom. The comparison of the alpha particle binding energy with the binding energy of the electron in a hydrogen atom is shown below. The nuclear binding energies are on the order of a million times greater than the electron binding energies of atoms.
Fission and fusion can yield energy
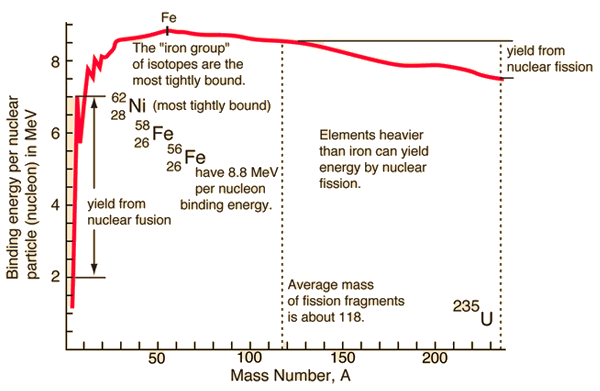
Nuclear Binding Energy Curve
The binding energy curve is obtained by dividing the total nuclear binding energy by the number of nucleons. The fact that there is a peak in the binding energy curve in the region of stability near iron means that either the breakup of heavier nuclei (fission) or the combining of lighter nuclei (fusion) will yield nuclei which are more tightly bound (less mass per nucleon).
The binding energies of nucleons are in the range of millions of electron volts compared to tens of eV for atomic electrons. Whereas an atomic transition might emit a photon in the range of a few electron volts, perhaps in the visible light region, nuclear transitions can emit gamma-rays with quantum energiesin the MeV range.
The iron limit
The buildup of heavier elements in the nuclear fusion processes in stars is limited to elements below iron, since the fusion of iron would subtract energy rather than provide it. Iron-56 is abundant in stellar processes, and with a binding energy per nucleon of 8.8 MeV, it is the third most tightly bound of the nuclides. Its average binding energy per nucleon is exceeded only by 58Fe and 62Ni, the nickel isotope being the most tightly bound of the nuclides.
Fission and Fusion Yields
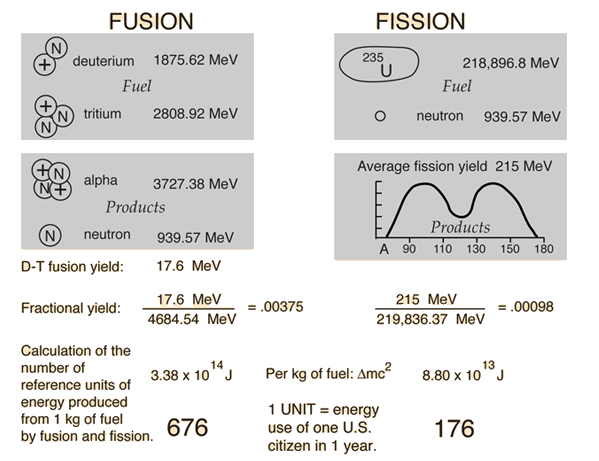
Deuterium-tritium fusion and uranium-235 fission are compared in terms of energy yield. Both the single event energy and the energy per kilogram of fuel are compared. Then they expressed in terms of a nominal per capita U.S. energy use: 5 x 1011 joules. This figure is dated and probably high, but it gives a basis for comparison. The values above are the total energy yield, not the energy delivered to a consumer.
Nuclear Fission
If a massive nucleus like uranium-235 breaks apart (fissions), then there will be a net yield of energy because the sum of the masses of the fragments will be less than the mass of the uranium nucleus. If the mass of the fragments is equal to or greater than that of iron at the peak of the binding energy curve, then the nuclear particles will be more tightly bound than they were in the uranium nucleus, and that decrease in mass comes off in the form of energy according to the Einstein equation. For elements lighter than iron, fusion will yield energy.
The fission of U-235 in reactors is triggered by the absorption of a low energy neutron, often termed a "slow neutron" or a "thermal neutron". Other fissionable isotopes which can be induced to fission by slow neutrons are plutonium-239, uranium-233, and thorium 232.
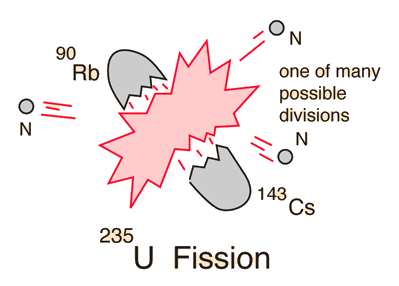
Uranium-235 Fission
In one of the most remarkable phenomena in nature, a slow neutron can be captured by a uranium-235 nucleus, rendering it unstable toward nuclear fission. A fast neutron will not be captured, so neutrons must be slowed down by moderation to increase their capture probability infission reactors. A single fision event can yield over 200 million times the energy of the neutron which triggered it!
Uranium Fuel
Natural uranium is composed of 0.72% U-235 (the fissionable isotope), 99.27% U-238, and a trace quantity 0.0055% U-234 . The 0.72% U-235 is not sufficient to produce a self-sustaining critical chain reaction in U.S. style light-water reactors, although it is used in Canadian CANDU reactors. For light-water reactors, the fuel must be enriched to 2.5-3.5% U-235.
Uranium is found as uranium oxide which when purified has a rich yellow color and is called "yellowcake". After reduction, the uranium must go through an isotope enrichment process. Even with the necessity of enrichment, it still takes only about 3 kg of natural uranium to supply the energy needs of one American for a year.
Fissionable Isotopes
While uranium-235 is the naturally occuring fissionable isotope, there are other isotopes which can be induced to fission by neutron bombardment. Plutonium-239 is also fissionable by bombardment with slow neutrons, and both it and uranium-235 have been used to make nuclear fission bombs. Plutonium-239 can be produced by "breeding" it from uranium-238.
Uranium-238, which makes up 99.3% of natural uranium, is not fissionable by slow neutrons. U-238 has a small probability for spontaneous fission and also a small probability of fission when bombarded with fast neutrons, but it is not useful as a nuclear fuel source. Some of the nuclear reactors at Hanford, Washington and the Savannah-River Plant (SC) are designed for the production of bomb-grade plutonium-239.
Thorium-232 is fissionable, so could conceivably be used as a nuclear fuel. The only other isotope which is known to undergo fission upon slow-neutron bombardment is uranium-233.
History of U-235 Fission
In the 1930s, German physicists/chemists Otto Hahn and Fritz Strassman attempted to create transuranic elements by bombarding uranium with neutrons. Rather than the heavy elements they expected, they got several unidentified products. When they finally identified one of the products as Barium-141, they were reluctant to publish the finding because it was so unexpected.
When they finally published the results in 1939, they came to the attention of Lise Meitner, an Austrian-born physicist who had worked with Hahn on his nuclear experiments. Upon Hitler's invasion of Austria, she had been forced to flee to Sweden where she and Otto Frisch, her nephew, continued to work on the neutron bombardment problem.
She was the first to realize that Hahn's barium and other lighter products from the neutron bombardment experiments were coming from the fission of U-235. Frisch and Meitner carried out further experiments which showed that the U-235 fission yielded an enormous amount of energy, and that the fission yielded at least two neutrons per neutron absorbed in the interaction. They realized that this made possible a chain reaction with an unprecedented energy yield.
Nuclear Fusion
If light nuclei are forced together, they will fuse with a yield of energy because the mass of the combination will be less than the sum of the masses of the individual nuclei. If the combined nuclear mass is less than that of iron at the peak of the binding energy curve, then the nuclear particles will be more tightly bound than they were in the lighter nuclei, and that decrease in mass comes off in the form of energy according to the Einstein relationship. For elements heavier than iron, fission will yield energy.
For potential nuclear energy sources for the Earth, the deuterium-tritium fusion reaction contained by some kind of magnetic confinement seems the most likely path. However, for the fueling of the stars, other fusion reactions will dominate.
 |  |
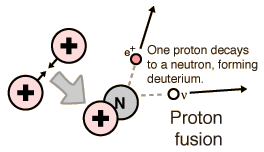Fusion Reactors
Reactors for nuclear fusion are of two main varieties, magnetic confinement reactors and inertial confinement reactors. The strategies for creating fusion reactors are largely dictated by the fact that the temperatures involved in nuclear fusion are far too high to be contained in any material container.
The strategy of the magnetic confinement reactor is to confine the hot plasma by means of magnetic fields which keep it perpetually in looping paths which do not touch the wall of the container. This is typified by the tokamak design, the most famous example of which is the TFTR at Princeton.
The strategy of the inertial confinement reactor is to put such high energy density into a small pellet of deuterium-tritium that it fuses in such a short time that it can't move appreciably. The most advanced test reactors involve laser fusion, particularly in the Shiva and Nova reactors at Lawrence Livermore Laboratories.
Conditions for Fusion
In addition to providing a sufficiently high temperature to enable the particles to overcome the Coulomb barrier, that temperature must be maintained for a sufficient confinement time and with a sufficient ion density in order to obtain a net yield of energy from a fusion reaction. The overall conditions which must be met for a yield of more energy than is required for the heating of the plasma are usually stated in terms of the product of ion density and confinement time, a condition called Lawson's criterion.
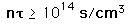 |  | deuterium-tritium fusion |
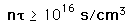 | deuterium-deuterium fusion |
Confinement Time for Fusion
Confinement time in nuclear fusion devices is defined as the time the plasma is maintained at a temperature above the critical ignition temperature. To yield more energy from the fusion than has been invested to heat the plasma, the plasma must be held up to this temperature for some minimum length of time. Calculations of that minimum time are
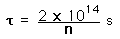 | deuterium-tritium fusion |
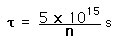 | deuterium-deuterium fusion |
Ion Density for Fusion
Even given a high enough temperature to overcome the coulomb barrier to nuclear fusion, a critical density of ions must be maintained to make the probability of collison high enough to achieve a net yield of energy from the reaction. The density required for a net energy yield is correlated with the confinement time for the hot plasma, so the minimum condition for a productive fusion reaction is typically stated in terms of the product of the ion density and confinement time, called Lawson's criterion. The calculated values are
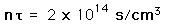 | deuterium-tritium fusion |
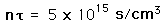 | deuterium-deuterium fusion |
Lawson's Criterion for Fusion
Once a critical ignition temperature for nuclear fusion has been achieved, it must be maintained at that temperature for a long enough confinement time at a high enough ion density to obtain a net yield of energy. In 1957, J. D. Lawson showed that the product of ion density and confinement time determined the minimum conditions for productive fusion, and that product is commonly called Lawson's criterion. Commonly quoted figures for this criterion are
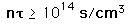| | deuterium-tritium fusion |
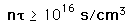| deuterium-deuterium fusion |
The closest approach to Lawson's criterion has been at the Tokamak Fusion Test Reactor (TFTR) at Princeton. It has reached ignition temperature and gotten very close to Lawson's criterion, although not at the same time.
Deuterium-Tritium Fusion
 |
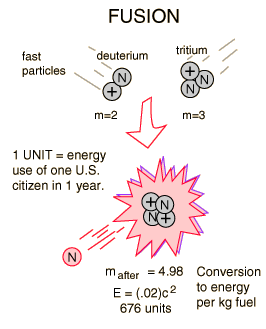The most promising of the hydrogen fusion reactions which make up the deuterium cycle is the fusion of deuterium and tritium.
The reaction yields 17.6 MeV of energy but requires a temperature of approximately 40 million Kelvins to overcome the coulomb barrier and ignite it. The deuterium fuel is abundant, but tritium must be either bred from lithium or gotten in the operation of the deuterium cycle.
|
Hydrogen Fusion Reactions
Even though a lot of energy is required to overcome the Coulomb barrier and initiate hydrogen fusion, the energy yields are enough to encourage continued research. Hydrogen fusion on the earth could make use of the reactions:
These reactions are more promising than the proton-proton fusion of the stars for potential energy sources. Of these the deuterium-tritium fusion appears to be the most promising and has been the subject of most experiments. In a deuterium-deuterium reactor, another reaction could also occur, creating a deuterium cycle:
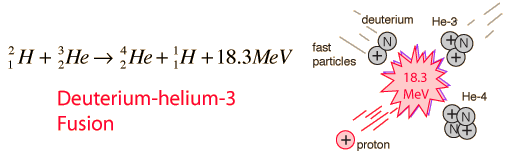
Deuterium Cycle of Fusion
The four fusion reactions which can occur with deuterium can be considered to form a deuterium cycle. The four reactions:
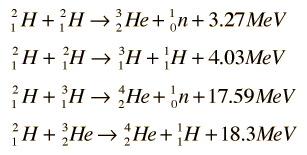
can be combined as
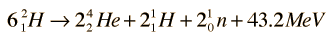
Tritium Breeding Deuterium
Tritium fusion is the most promising of the hydrogen fusion reactions, but no tritium occurs in nature since it has a 10 year half-life. The most promising source of tritium seems to be the breeding of tritium from lithium-6 by neutron bombardment with the reaction
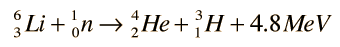
which can be achieved by slow neutrons. This would occur if lithium were used as the coolant and heat transfer medium around the reaction chamber of a fusion reactor. Lithium-6 makes up 7.4% of natural lithium. While this constitutes a sizable supply, it is the limiting resource for the D-T process since the supply of deuterium fuel is virtually unlimited. With fast neutrons, tritium can be bred from the more abundant Li-7:
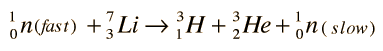
Deuterium Source
Since the most practical nuclear fusion reaction for power generation seems to be the deuterium-tritium reaction, the sources of these fuels are important. The deuterium part of the fuel does not pose a great problem because about 1 part in 5000 of the hydrogen in seawater is deuterium. This amounts to over 1015tons of deuterium.
Viewed as a potential fuel for a fusion reactor, a gallon of seawater could produce as much energy as 300 gallons of gasoline. The tritium part of the fuel is more problematic - there is no sizable natural source since tritium is radioactive with a halflife of about 10 years. It would have to be obtained by breeding the tritium from lithium
Sem comentários:
Enviar um comentário