Annihilation
Annihilation is defined as "total destruction" or "complete obliteration" of an object;[1] having its root in the Latin nihil (nothing). A literal translation is "to make into nothing".
In physics, the word is used to denote the process that occurs when a subatomic particle collides with its respective antiparticle, such as an electron colliding with a positron, illustrated here.[2] Since energy and momentum must be conserved, the particles are simply transformed into new particles. They do not disappear from existence.
Antiparticles have exactly opposite additive quantum numbers from particles, so the sums of all quantum numbers of the original pair are zero. Hence, any set of particles may be produced whose total quantum numbers are also zero as long as conservation of energy and conservation of momentum are obeyed. When a particle and its antiparticle collide, their energy is converted into a force carrier particle, such as a gluon, W/Z force carrier particle, or a photon. These particles are afterwards transformed into other particles.[3]
During a low-energy annihilation, photon production is favored, since these particles have no mass. However, high-energy particle colliders produce annihilations where a wide variety of exotic heavy particles are created.
Crossing Symmetry
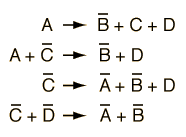
Compton scattering: γ + e- → e- + γ
Pair annihilation: e- + e+ → γ + γ
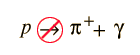
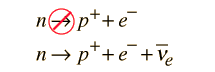
Crossing Symmetry
If a particle interaction
is observed to occur, then related interactions can be anticipated from the fact that any of the particles can be replaced by its antiparticle on the other side of the interaction. This is commonly known as "crossing symmetry". The observation of the above interaction implies the existence of the following interactions.
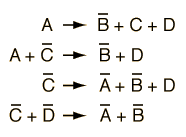
The overbar indicates the antiparticle. Crossing symmetry applies to all known particles, including the photon which is its own antiparticle. One example of the crossing principle is that of the relation between Compton scattering and electron-positron annihilation.
  | Compton Scattering
Arthur H. Compton observed the scattering of x-rays from electrons in a carbon target and found scattered x-rays with a longer wavelength than those incident upon the target. The shift of the wavelength increased with scattering angle according to the Compton formula:
Compton explained and modeled the data by assuming a particle (photon) nature for light and applying conservation of energy and conservation of momentum to the collision between the photon and the electron. The scattered photon has lower energy and therefore a longer wavelength according to the Planck relationship.
|
At a time (early 1920's) when the particle (photon) nature of light suggested by the photoelectric effect was still being debated, the Compton experiment gave clear and independent evidence of particle-like behavior. Compton was awarded the Nobel Prize in 1927 for the "discovery of the effect named after him"
.
Positron Annihilation.
The positron is the antiparticle of the electron, and when a positron enters any normal matter, it will find an abundant supply of electrons with which to annihilate. The energy released by the annihilation forms two highly energetic gamma rays, and if one assumes that the momenta of the positron and electron before the annihilation, the two gamma ray photons must travel in opposite directions in order to conserve momentum.
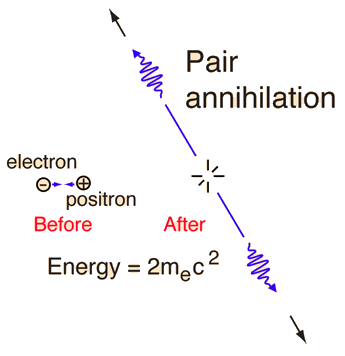 | These coincident gamma rays at 180 degrees provide a useful analysis tool. For one thing, eliminating all gamma events which are not coincident at 180 degrees improves the signal-to-noise ratio of experiments using positron annihilation. Another interesting application is the use of the coincident gammas to locate the source by back projecting. This is used in medical PET scans. |
Totalitarian Principle
From what we observe with massive particles, it would seem that any localized particle of finite mass should be unstable, since the decay into several smaller particles provides many more ways to distribute the energy, and thus would have higher entropy. Some have adopted the description "totalitarian principle" for this situation. It might be stated as "every process that is not forbidden must occur". From this point of view, any decay process which is expected but not observed must be prevented from occuring by some conservation law. This approach has been fruitful in helping to determine the rules for particle decay.
For example, with just conservation of energy and charge considered, one might expect a proton to decay into a positive pion plus a gamma ray to take away excess energy and conserve momentum:
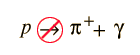
The fact that neither this nor any other decay of the proton is observed suggests that the decay of the proton is forbidden by a strong conservation principle. This principle is called the conservation of baryon number, and no observed particle decays violate it. The proton does not decay because it is the least massive baryon, and has nowhere to go.
Another decay which was expected on energy and charge grounds was the decay of the neutron into a proton and an electron. The decay of the neutron is observed, but the fact that the electron does not have a definite energy implies that there is a third particle in the decay, the antineutrino.
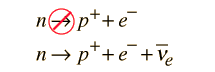
The fact that the first of these decays did not occur suggested a prohibiting conservation law, which is called the conservation of lepton number.
Since the strengths of the interactions associated with particle decay descend in the order strong, electromagnetic and weak, it might be presumed that the strongest interaction would lead to the shortest lifetime, and that is what is observed. From experiments we can establish time regimes for the three types of interactions.
| Strong | |
| Electromagnetic | |
| Weak |
In the spirit of the "totalitarian principle", if you observed a decay in the 10-16 s range you might guess that it is electromagnetic, and that some principle prevented it decay by the strong interaction. A 10-10 s decay suggests that both strong and electromagnetic are somehow blocked.
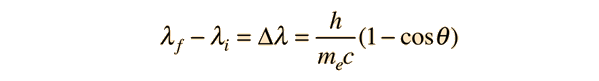
Sem comentários:
Enviar um comentário