Wave Nature of Electron
As a young student at the University of Paris, Louis De Broglie ( Nobel Prize in 1929) had been impacted by relativity and the photoelectric effect, both of which had been introduced in his lifetime. In his 1924 PhD thesis he postulated the wave nature of electrons and suggested that all matter has wave properties.
This concept is known as wave-particle duality or the de Broglie hypothesis.The photoelectric effect pointed to the particle properties of light, which had been considered to be a wave phenomenon.
He wondered if electons and other "particles" might exhibit wave properties. The application of these two new ideas to light pointed to an interesting possibility:
 |
| Louis De Broglie |
This concept is known as wave-particle duality or the de Broglie hypothesis.The photoelectric effect pointed to the particle properties of light, which had been considered to be a wave phenomenon.
He wondered if electons and other "particles" might exhibit wave properties. The application of these two new ideas to light pointed to an interesting possibility:
Confirmation of the De Broglie hypothesis came in the Davisson- Germer experiment.
Examples of Electron Waves
Two specific examples supporting the wave nature of electrons as suggested in the DeBroglie hypothesis are the discrete atomic energy levels and the diffraction of electrons from crystal planes in solid materials. In the Bohr model of atomic energy levels, the electron waves can be visualized as "wrapping around" the circumference of an electron orbit in such a way as to experience constructive interference.

Click on either example for further details.
The wave nature of the electron must be invoked to explain the behavior of electrons when they are confined to dimensions on the order of the size of an atom. This wave nature is used for the quantum mechanical "particle in a box" and the result of this calculation is used to describe the density of energy states for electrons in solids.
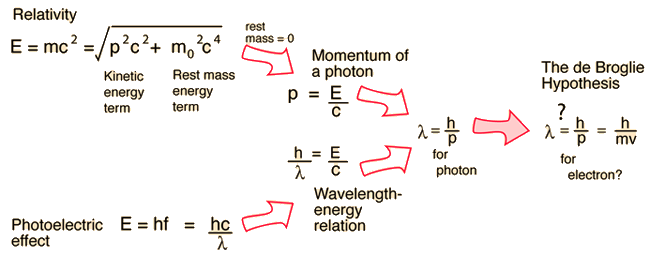
De Broglie Hypothesis
Suggested by De Broglie in about 1923, the path to the wavelength expression for a particle is by analogy to the momentum of a photon. Starting with theEinstein formula:
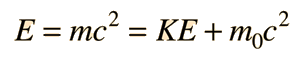
| Another way of expressing this is | 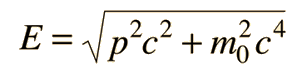 |
The momentum-wavelength relationship for a photon can then be derived and this DeBroglie wavelength relationship applies to other particles as well.
De Broglie Wavelengths

If you explore the wavelength values for ordinary macroscopic objects like baseballs, you will find that their DeBroglie wavelengths are ridiculously small. Comparison of the power of ten for the wavelength will show what the wavelengths of ordinary objects are much smaller than a nucleus. The implication is that for ordinary objects, you will never see any evidence of their wave nature, and they can be considered to be particles for all practical purposes.
De Broglie Wavelengths
You may enter values in any of the boxes. When you have finished entering data, click on the quantity you wish to calculate in the formula above. Wavelength values will be reconciled, but no further calculation will be done until you select which item you wish to calculate. Caution! This calculation is non-relativistic and accurate only for speeds much less than the speed of light. For speeds over a tenth of the speed of light a relativistic calculation should be used.
If you explore the wavelength values for ordinary macroscopic objects like baseballs, you will find that their De Broglie wavelengths are ridiculously small. Comparison of the power of ten for the wavelength will show what the wavelengths of ordinary objects are much smaller than a nucleus. The implication is that for ordinary objects, you will never see any evidence of their wave nature, and they can be considered to be particles for all practical purposes.
De Broglie Wavelength
A convenient form for the De Broglie wavelength expression is
This is particularly appropriate for comparison with photon wavelengths since for the photon, pc=E and a 1 eV photon is seen immediately to have a wavelength of 1240 nm. For massive particles with kinetic energy KE which is much less than their rest mass energies:
For an electron with KE = 1 eV and rest mass energy 0.511 MeV, the associated DeBroglie wavelength is 1.23 nm, about a thousand times smaller than a 1 eV photon. (This is why the limiting resolution of an electron microscope is much higher than that of an optical microscope.)
The following calculation uses the full relativistic expressions for kinetic energy, etc.
Caution! Since this calculation was designed for speeds which are a significant fraction of the speed of light, it may lose some accuracy for very low speeds. Under those conditions, small differences between large numbers occur in the calculations. For low speed calculations like the baseball example, it might be more accurate to use the non-relativistic calculation.
 which reduces to E = pc for photons . The quantity pc is proportional to the relativistic momentum but has energy units, and it is useful in many high energy calculations. Using 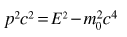 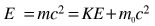 an expression for pc in terms of the relativistic kinetic energy can be obtained: 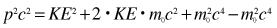 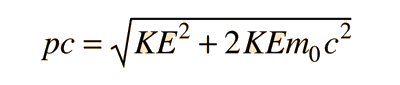 For most ordinary processes the kinetic energy is much less than the rest mass energy, so the first term can usually be neglected. This leads to the useful approximation: 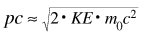
For less than 1% error this requires electron energies over 3.2 MeV and proton energies over 5.8 GeV. A useful application of the quantity pc is in the calculation of the velocity as a fraction of c.
with the limiting case applying for the momentum of ph Davisson-Germer Experiment 
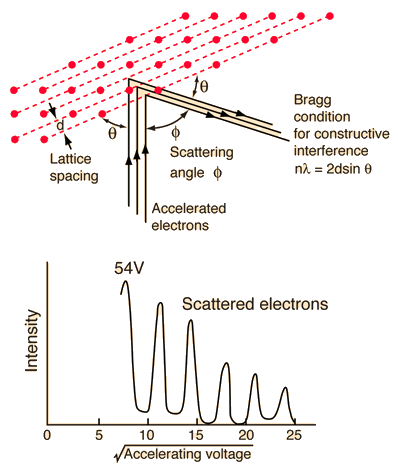
This experiment demonstrated the wave nature of the electron, confirming the earlier hypothesis of deBroglie. Putting wave-particle duality on a firm experimental footing, it represented a major step forward in the development of quantum mechanics. The Bragg law for diffraction had been applied to x-ray diffraction, but this was the first application to particle waves.
Davisson-Germer Experiment
The electron beam was directed at the nickel target, which could be rotated to observe angular dependence of the scattered electrons. Their electron detector (called a Faraday box) was mounted on an arc so that it could be rotated to observe electrons at different angles. It was a great surprise to them to find that at certain angles there was a peak in the intensity of the scattered electron beam. This peak indicated wave behavior for the electrons, and could be interpreted by the Bragg law to give values for the lattice spacing in the nickel crystal.
The experimental data above, reproduced above Davisson's article, shows repeated peaks of scattered electron intensity with increasing accelerating voltage. This data was collected at a fixed scattering angle. Using the Bragg law, the deBroglie wavelength expression, and the kinetic energy of the accelerated electrons gives the relationship
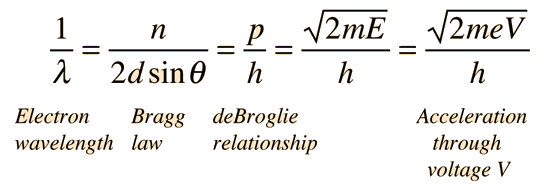
In the historical data, an accelerating voltage of 54 volts gave a definite peak at a scattering angle of 50°. The angle theta in the Bragg law corresponding to that scattering angle is 65°, and for that angle the calculated lattice spacing is 0.092 nm. For that lattice spacing and scattering angle, the relationship for wavelength as a function of voltage is empirically

Trying this relationship for n=1,2,3 gives values for the square root of voltage 7.36, 14.7 and 22, which appear to agree with the first, third and fifth peaks above. Then what gives the second, fourth and sixth peaks? Perhaps they originate from a different set of planes in the crystal. Those peaks satisfy a sequence 2,3,4, suggesting that the first peak of that series would have been at 5.85 . That corresponds to an electron wavelength of 0.21 nm and a lattice spacing of 0.116 nm ?? I don't know if that makes sense. I need to look at the original article.
|

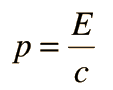
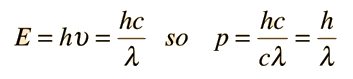


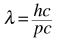
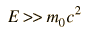
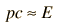
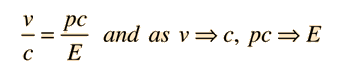
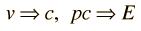
Sem comentários:
Enviar um comentário