X-Rays
X-ray was the name given to the highly penetrating rays which emanated when high energy electrons struck a metal target. Within a short time of their discovery, they were being used in medical facilities to image broken bones. We now know that they are high frequency electromagnetic rays which are produced when the electrons are suddenly decelerated - these rays are called bremsstrahlung radiation, or "braking radiation".
X-rays are also produced when electrons make transitions between lower atomic energy levels in heavy elements. X-rays produced in this way have have definite energies just like other line spectra from atomic electrons. They are called characteristic x-rays since they have energies determined by the atomic energy levels. In interactions with matter, x-rays are ionizing radiation and produce physiological effects which are not observed with any exposure of non-ionizing radiation, such as the risk of mutations or cancer in tissue.
Astronomical observations in the X-ray region of the spectrum are obtained with the Chandra X-ray Observatory.
X-rays are part of the
Electromagnetic spectrum
Frequencies: 3 x 1016 Hz upward Wavelengths: 10 nm - > downward Quantum energies: 124 eV -> upward
Electromagnetic spectrum |
|
Characteristic X-Rays
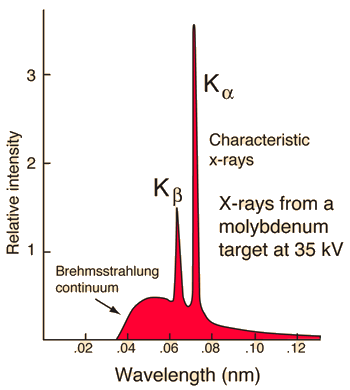 |
Characteristic x-rays are emitted from heavy elements when their electrons make transitions between the lower atomic energy levels. The characteristic x-rays emission which shown as two sharp peaks in the illustration at left occur when vacancies are produced in the n=1 or K-shell of the atom and electrons drop down from above to fill the gap.
The x-rays produced by transitions from the n=2 to n=1 levels are called K-alpha x-rays, and those for the n=3->1 transiton are called K-beta x-rays.
Transitions to the n=2 or L-shell are designated as L x-rays (n=3->2 is L-alpha, n=4->2 is L-beta, etc. ). The continuous distribution of x-rays which forms the base for the two sharp peaks at left is called"bremsstrahlung" radiation.
|
X-ray production typically involves bombarding a metal target in an x-ray tube with high speed electrons which have been accelerated by tens to hundreds of kilovolts of potential. The bombarding electrons can eject electrons from the inner shells of the atoms of the metal target. Those vacancies will be quickly filled by electrons dropping down from higher levels, emitting x-rays with sharply defined frequencies associated with the difference between the atomic energy levels of the target atoms.
The frequencies of the characteristic x-rays can be predicted from the Bohr model . Moseley measured the frequencies of the characteristic x-rays from a large fraction of the elements of the periodic table and produces a plot of them which is now called a "Moseley plot".
Characteristic x-rays are used for the investigation of crystal structure by x-ray diffraction. Crystal lattice dimensions may be determined with the use of Bragg's law in a Bragg spectrometer.
X-ray Transitions
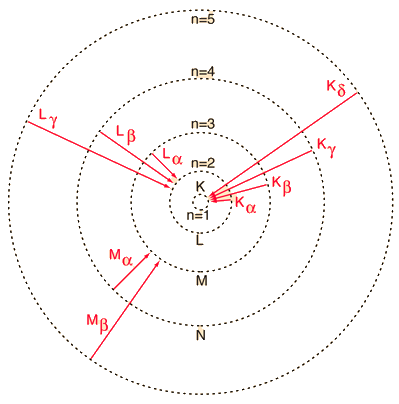 |
Electron transitions to lower atomic levels in heavy atoms have quantum energies which place them in thex-ray region of the electromagnetic spectrum.
The x-ray emissions associated with these transitions are called characteristic x-rays. The labels on the illustration show the historical labeling of characteristic x-ray transitions.
|
The frequencies of the characteristic x-rays can be predicted from the Bohr model . Moseley measured the frequencies of the characteristic x-rays from a large fraction of the elements of the periodic table and produces a plot of them which is now called a "Moseley plot".
Bremsstrahlung X-Rays
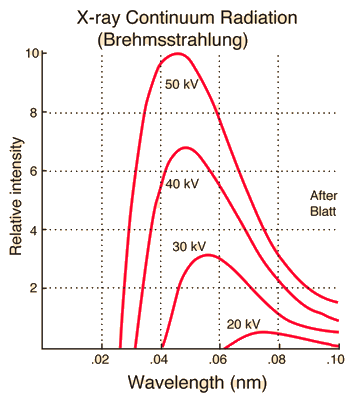
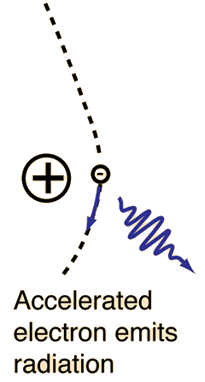
"Bremsstrahlung" means "braking radiation" and is retained from the original German to describe the radiation which is emitted when electrons are decelerated or "braked" when they are fired at a metal target. Accelerated charges give off electromagnetic radiation, and when the energy of the bombarding electrons is high enough, that radiation is in the x-ray region of the electromagnetic spectrum. It is characterized by a continuous distribution of radiation which becomes more intense and shifts toward higher frequencies when the energy of the bombarding electrons is increased.
The curves above are from the 1918 data of Ulrey, who bombarded tungsten targets with electrons of four different energies. The bombarding electrons can also eject electrons from the inner shells of the atoms of the metal target, and the quick filling of those vacancies by electrons dropping down from higher levels gives rise to sharply defined characteristic x-rays.
X-ray Tube
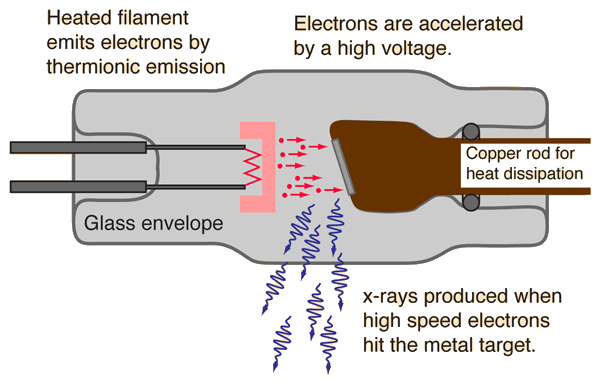
X-rays for medical diagnostic procedures or for research purposes are produced in a standard way: by accelerating electrons with a high voltage and allowing them to collide with a metal target. X-rays are produced when the electrons are suddenly decelerated upon collision with the metal target; these x-rays are commonly called brehmsstrahlung or "braking radiation".
If the bombarding electrons have sufficient energy, they can knock an electron out of an inner shell of the target metal atoms. Then electrons from higher states drop down to fill the vacancy, emitting x-ray photons with precise energies determined by the electron energy levels. These x-rays are called characteristic x-rays.
Moseley's Modeling of X-ray Frequencies
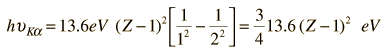
The implication of this relationship is that the single electron in the K-shell before the emission is almost 100% effective in shielding the nucleus so that the electron from the L-shell sees an effective nuclear charge of Z-1. We can use this relationship to calculate approximate quantum energies and wavelengths for K-alpha x-rays.
For example, this calculation for Z=42 gives a wavelength of 0.0722 nm for the molybdenum K-alpha x-ray whereas the measured value is 0.0707 nm. So the agreement is reasonable for K-alpha x-rays even though the upper level of the transition experiences some shielding which is unaccounted for in this model.
For transitions ending in higher shells, the shielding situation becomes much more complex. From the Bohr model, we might write an equation for an L-alpha x-ray as
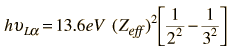
Moseley found that his data for the L-alpha x-rays fit the empirical relationship
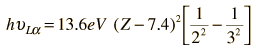
so that the best fit to the data was with Z-7.4, indicating a shielding corresponding to 7.4 electrons on the average inside the M-shell from which the electron originated.
 |
X-Rays medical equipment |
Moseley's Investigation of X-rays
Henry G. J. Moseley (1887-1915) was described by Rutherford as his most talented student. When he was in his early 20's, he measured and plotted the x-ray frequencies for about 40 of the elements of the periodic table. He showed that the K-alpha x-rays followed a straight line when the atomic number Z versus the square root of frequency was plotted. His data (the Moseley plot) is still a standard feature of physics textbooks.
At the time when he was working, most physicists regarded the atomic weight A as the key to ordering the periodic table, rather than the atomic number Z. For example, nickel, with atomic weight 58.7 was placed ahead of cobalt, atomic weight 58.9, in the periodic table. Moseley's work showed that cobalt had an atomic number of 27 and nickel 28. Potassium (Z=19, A=39.10) and Argon (Z=18, A=39.95) were also reversed when listed by atomic weight order.
Moseley predicted the existence of an element at Z=72 (Hafnium) which was subsequently discovered in Bohr's laboratory in Copenhagen. Moseley volunteered for combat duty during World War I and was killed in action at age 27 during the attack on Gallipoli in the Dardenelles.
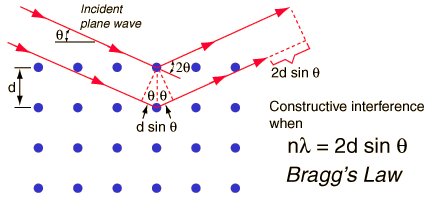
When x-rays are scattered from a crystal lattice, peaks of scattered intensity are observed which correspond to the following conditions:
- The angle of incidence = angle of scattering.
- The pathlength difference is equal to an integer number of wavelengths.
The condition for maximum intensity contained in Bragg's law above allow us to calculate details about the crystal structure, or if the crystal structure is known, to determine the wavelength of the x-rays incident upon the crystal.
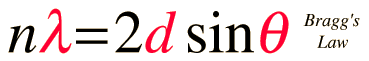
This calculation is designed to calculate wavelength, crystal plane separation or diffraction angle. After entering data, click on the symbol of the quantity you wish to calculate in the active graphic above. Default data will be entered for any unspecified quantity, but all values can be changed.
Bragg Spectrometer
Much of our knowledge about crystal structure and the structure of molecules as complex as DNA in crystalline form comes from the use of x-rays in x-ray diffraction studies. A basic instrument for such study is the Bragg spectrometer.
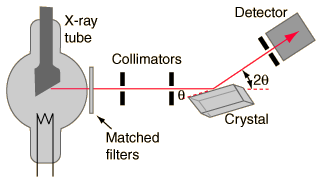
To obtain nearly monochromatic x-rays, an x-ray tube is used to produce characteristic x-rays. In order to eliminate as much of the brehmsstrahlung continuum radiation as possible, matched filters are used in the x-ray beam to optimize the fraction of the energy which is in the K-alpha line. Such filters use elements just above and just below the metal in the x-ray target, making use of the strong "absorption edges" just above and below the K-alpha energy of the target metal.
The x-rays are collimated with apertures in a strong x-ray absorber (usually lead) and the narrow resulting x-ray beam is allowed to strike the crystal to be studied. The spectrometer arrangement couples the rotation of the crystal with the rotation of the detector so that the angle of rotation of the detector is twice that of the crystal. This satisfies the conditions of Bragg's law for diffraction of the x-rays from the crystal lattice planes.
Compton Scattering Data
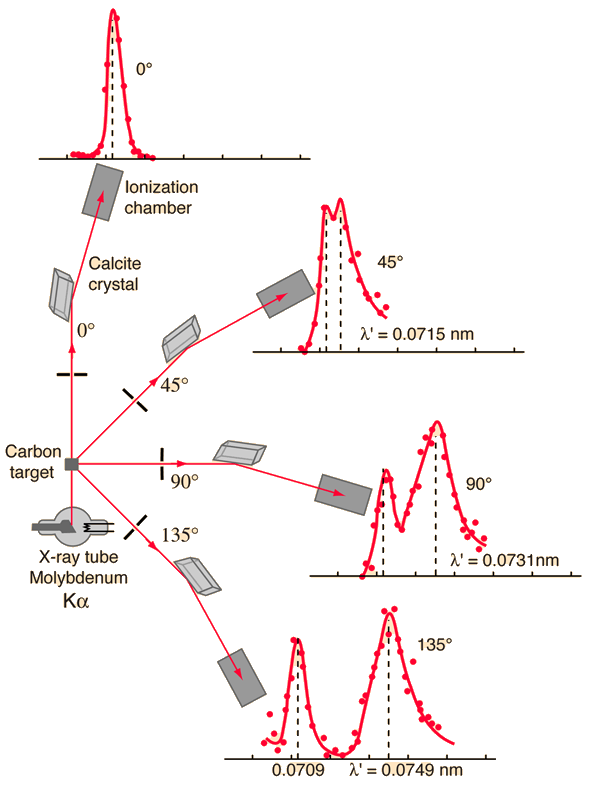
The scattering of photons from charged particles is called Compton scattering after Arthur Compton who was the first to measure photon-electron scattering in 1922. When the incoming photon gives part of its energy to the electron, then the scattered photon has lower energy and according to the Planck relationship has lower frequency and longer wavelength. The wavelength change in such scattering depends only upon the angle of scattering for a given target particle.(A. H. Compton, Phys. Rev. 21, 483; 22, 409 (1923))

Examination of the Compton scattering formula shows that the scattered wavelength depends upon the angle of scattering and also the mass of the scatterer. For scattering from stationary electrons, the formula gives a wavelength of 0.0733 nm for scattering at 90 degrees. That is consistent with the right-hand peak in the illustration above. The peak which is near the original x-ray wavelength is considered to be scattering off inner electrons in the carbon atoms which are more tightly bound to the carbon nucleus.
This causes the entire atom to recoil from the x-ray photon, and the larger effective scattering mass proportionally reduces the wavelength shift of the scattered photons. Putting the entire carbon nuclear mass into the scattering equation yields a wavelength shift almost 22,000 times smaller than that for an unbound electron, so those scattered photons are not seen to be shifted.
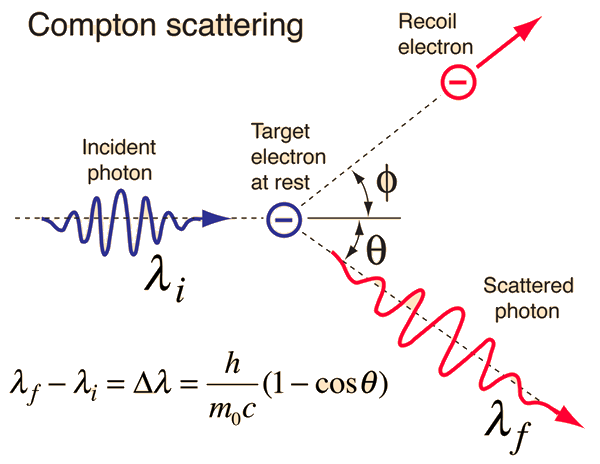
The scattering of photons from charged particles is called Compton scattering after Arthur Compton who was the first to measure photon-electron scattering in 1922. When the incoming photon gives part of its energy to the electron, then the scattered photon has lower energy and according to the Planck relationship has lower frequency and longer wavelength. The wavelength change in such scattering depends only upon the angle of scattering for a given target particle. The constant in the Compton formula above can be written
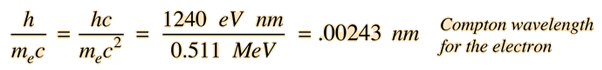
and is called the Compton wavelength for the electron. The formula presumes that the scattering occurs in the rest frame of the electron.
This exploration is designed to accept values for the input wavelength or energy and the angle of scattering. Unspecified parameters will default to the case of molybdenum K-alpha xrays scattering at 90 degrees, one of Compton's historical results. Any of these input values can be changed.
If a high energy photon interacts with an electron, the interaction can be described by the Compton scattering relationship or by the 4-vector formulation of relativistic momentum. As a specific example, consider a 10GeV photon in a head-on collision with an electron at rest.
If we apply the Compton formula
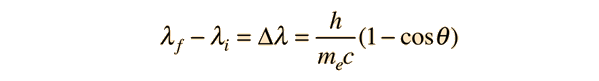
with l = h/p for a back-scattered photon where q = 180°, this relationship becomes
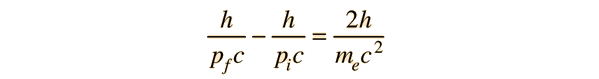

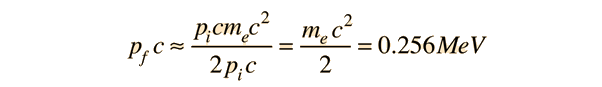
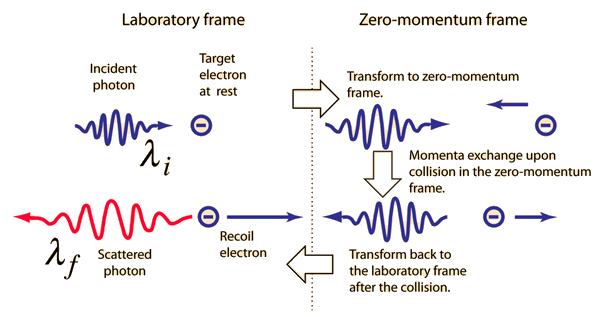
The conceptual description that leads you to the conclusion that the electron has most of the energy after the conclusion involves transforming the momenta to the zero-momentum frame, which diminishes the momentum of the photon while increasing that of the electron. Then the momenta exchange upon collision in the zero momentum frame. Then you make the reverse transformation which further reduces the magnitude of the photon momentum while increasing the momentum of the electron. For the extreme example used here, the electron gets most of the energy.
The transformation to the zero-momentum frame, however, is not a matter of transforming the photon down to 5 GeV and giving the electron a momentum -5GeV/c as you might expect. The transformation is much more drastic. It can be accomplished by using the energy and momentum as a 4-vector and doing the necessary Lorentz transformation.
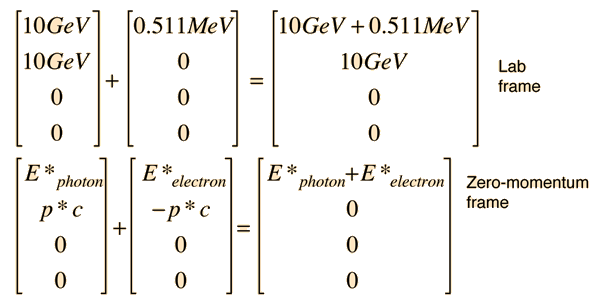
The tool to be used is the invariance of the length of the 4-vector upon transformation. Evaluated in the laboratory frame, it is
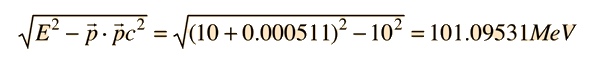
Then in the zero-momentum frame, this energy is divided between the photon and the electron in such a way that their momenta are equal in magnitude. Using the relativistic energy relationship to express the length of the 4-vector in terms of the momenta gives


This allows us to set up the energy/momentum transformation.
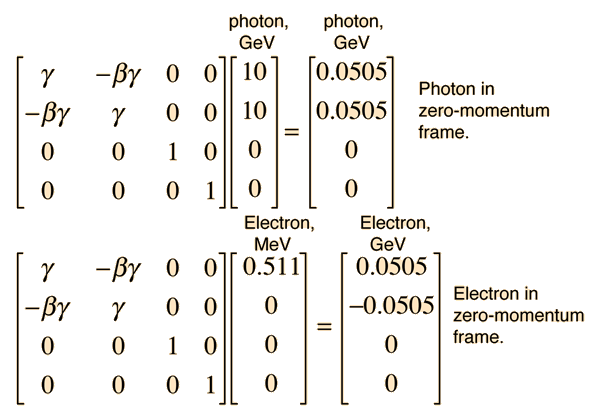
This transformation does indeed give us zero momentum and conserve energy. Reversing the sign of b should take us back to the laboratory frame.

This transformation gives us the same results that were obtained by the Compton scattering approach.
Discovery of Radioactivity
Radioactivity was discovered by A. H. Becquerel in 1896. The radiation was classified by E. Rutherford as alpha, beta, and gamma rays according to their ability to penetrate matter and ionize air.
Gamma-Rays
The term gamma ray is used to denote electromagnetic radiation from the nucleus as a part of a radioactive process. The energy of nuclear radiation is extremely high because such radiation is born in the intense conflict between the nuclear strong force and the electromagnetic force, the two strongest basic forces. The gamma ray photon may in fact be identical to an x-ray, since both are electromagnetic rays; the terms x-ray and gamma rays are statements about origin rather than implying different kinds of radiation.
In interactions with matter, gamma rays are ionizing radiation and producephysiological effects which are not observed with any exposure of non-ionizing radiation, such as the risk of mutations or cancer in tissue.
| Frequencies: typically >1020 Hz |
| Wavelengths: typically < 10-12 m |
| Quantum energies: typically >1 MeV |
Gamma Radioactivity
 |
Gamma radioactivity is composed of electromagnetic rays. It is distinguished from x-rays only by the fact that it comes from the nucleus. Most gamma rays are somewhat higher in energy than x-rays and therefore are very penetrating.
It is the most useful type of radiation for medical purposes, but at the same time it is the most dangerous because of its ability to penetrate large thicknesses of material.
|  |
Other Radioactive Processes
While the most common types of radioactive decay are by alpha, beta, and gamma radiation, several other varieties of radioactivity occur:
Electron capture: A parent nucleus may capture one of its own electrons and emit a neutrino. This is exhibited in the potassium-argon decay.
Positron or positive beta decay: Positron emission is called beta decay because the characteristics of electron or positron decay are similar. They both show a characteristic energy spectrum because of the emission of a neutrino or antineutrino.
Internal conversion is the use of electromagnetic energy from the nucleus to expel an orbital electron from the atom.
Internal Conversion
While the most common types of radioactive decay are by alpha, beta, and gamma radiation, several other varieties of radioactivity occur:
Electron capture: A parent nucleus may capture one of its own electrons and emit a neutrino. This is exhibited in the potassium-argon decay.
Positron or positive beta decay: Positron emission is called beta decay because the characteristics of electron or positron decay are similar. They both show a characteristic energy spectrum because of the emission of a neutrino or antineutrino.
Internal conversion is the use of electromagnetic energy from the nucleus to expel an orbital electron from the atom.
Electron Capture
Electron capture is one form of radioactivity. A parent nucleus may capture one of its orbital electrons and emit a neutrino. This is a process which competes with positron emission and has the same effect on the atomic number. Most commonly, it is a K-shell electron which is captured, and this is referred to as K-capture. A typical example is
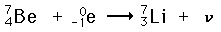
In the middle range of the periodic table, those isotopes which are lighter than the most stable isotopes tend to decay by electron capture, and those heavier decay by negative beta decay. An example of this pattern is seen with silver isotopes, with two stable isotopes plus one of lower mass which decays by electron capture and one of heavier mass which decays by beta emission.
Internal conversion is another electromagnetic process which can occur in the nucleus and which competes with gamma emission. Sometimes the multipole electric fields of the nucleus interact with orbital electrons with enough energy to eject them from the atom. This process is not the same as emitting a gamma ray which knocks an electron out of the atom. It is also not the same as beta decay, since the emitted electron was previously one of the orbital electrons, whereas the electron in beta decay is produced by the decay of a neutron.
An example used by Krane is that of 203Hg, which decays to 203Tl by beta emission, leaving the 203Tl in an electromagnetically excited state. It can proceed to the ground state by emitting a 279.190 keV gamma ray, or by internal conversion. In this case the internal conversion is more probable. Since the internal conversion process can interact with any of the orbital electrons, the result is a spectrum of internal conversion electrons which will be seen as superimposed upon the electron energy spectrum of the beta emission.
The energy yield of this electromagnetic transition can be taken as 279.190 keV, so the ejected electrons will have that energy minus their binding energy in the 203Tl daughter atom.
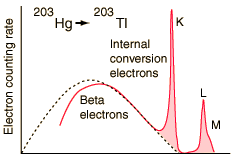 | Electron emissions from the Hg-203 to Tl-203 decay, measured by A. H. Wapstra, et al., Physica 20, 169 (1954). |
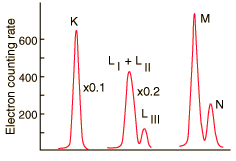 | At higher resolution, the internal conversion electrons from the L, M and N shells can be resolved. Z. Sujkowski, Ark. Fys. 20, 243 (1961). |
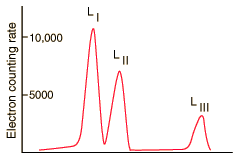 | At even higher resolution, the three L shells can be resolved. From C. J. Herrlander and R. L. Graham, Nucl. Phys. 58, 544 (1964). |
The resolution of the electron detection is good enough that such internal conversion electron spectra can be used to study the binding energies of the electrons in heavy atoms. In this case, the measured electron energies can be subtracted from the transition energy as indicated by the gamma emission, 279.190 keV.
| 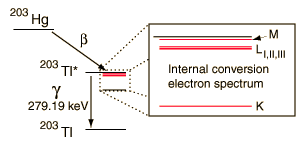 | ||||||||||||
In addition to information from the internal conversion electrons about the binding energies of the electrons in the daughter atom, the relative intensities of these internal conversion electron peaks can give information about the electric multipole character of the nucleus.
Cosmic rays
Cosmic ray is the term given to high energy radiation which strikes the Earth from space. Some of them have ultrahigh energies in the range 100 - 1000 TeV. Such extreme energies come from only a few sources like Cygnus X-3. The peak of the energy distribution is at about 0.3 GeV.
The intensity of cosmic radiation increases with altitude, indicating that it comes from outer space. It changes with latitude, indicating that it consists at least partly of charged particles which are affected by the earth's magnetic field.
The illustration at right shows that the detected cosmic ray flux peaks at about 15 km in altitude and then drops sharply (note the logarithmic scale on the altitude). This kind of variation was discovered by Pfotzer in 1936.
It suggests that the detection method used was mainly detecting secondary particles rather than the primary particles reaching the Earth from space.
|  |
Analysis of the particle populations in cosmic rays yields hints about their origin.
Magnetic Field of the Earth
The Earth's magnetic field is similar to that of a bar magnet tilted 11 degrees from the spin axis of the Earth. The problem with that picture is that the Curie temperature of iron is about 770 C . The Earth's core is hotter than that and therefore not magnetic. So how did the Earth get its magnetic field?
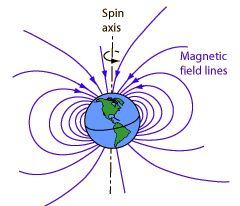 |
Magnetic fields surround electric currents, so we surmise that circulating electic currents in the Earth's molten metalic core are the origin of the magnetic field. A current loop gives a field similar to that of the earth. The magnetic field magnitude measured at the surface of the Earth is about half a Gauss and dips toward the Earth in the northern hemisphere. The magnitude varies over the surface of the Earth in the range 0.3 to 0.6 Gauss.
|
The Earth's magnetic field is attributed to a dynamo effect of circulating electric current, but it is not constant in direction. Rock specimens of different age in similar locations have different directions of permanent magnetization. Evidence for 171 magnetic field reversals during the past 71 million years has been reported.
Although the details of the dynamo effect are not known in detail, the rotation of the Earth plays a part in generating the currents which are presumed to be the source of the magnetic field. Mariner 2 found that Venus does not have such a magnetic field although its core iron content must be similar to that of the Earth. Venus's rotation period of 243 Earth days is just too slow to produce the dynamo effect.
Interaction of the terrestrial magnetic field with particles from the solar wind sets up the conditions for the aurora phenomena near the poles.
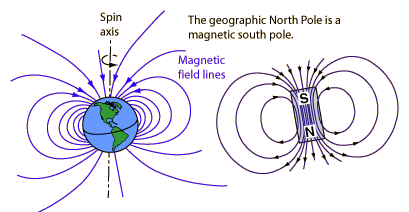
The north pole of a compass needle is a magnetic north pole. It is attracted to the geographic North Pole, which is a magnetic south pole (opposite magnetic poles attract).
The Dynamo Effect
The simple question "how does the Earth get its magnetic field?" does nothave a simple answer. It does seem clear that the generation of the magnetic field is linked to the rotation of the earth, since Venus with a similar iron-core composition but a 243 Earth-day rotation period does not have a measurable magnetic field.
It certainly seems plausible that it depends upon the rotation of the fluid metallic iron which makes up a large portion of the interior, and the rotating conductor model leads to the term "dynamo effect" or "geodynamo", evoking the image of an electric generator.
Convection drives the outer-core fluid and it circulates relative to the earth. This means the electrically conducting material moves relative to the earth's magnetic field. If it can obtain a charge by some interaction like friction between layers, an effective current loop could be produced. The magnetic field of a current loop could sustain the magnetic dipole type magnetic field of the earth. Large-scale computer models are approaching a realistic simulation of such a geodynamo.
Almost 90% of the cosmic rays which strike the Earth's atmosphere are protons (hydrogen nuclei) and about 9% are alpha particles. Electrons amount to about 1% according to Chaisson & McMillan. There is a small fraction of heavier particles which yield some interesting information. About 0.25% are light elements (lithium, beryllium and boron), but this is greatly enriched over the abundance of these elements in the universe which is only about one billionth!
From this evidence it is implied that these light elements have been produced as fragments in high-speed collisions when primary cosmic ray particles like protons strike elements like carbon and oxygen in the very tenuous matter in interstellar space. Attempts have been made to model how much ordinary matter would be required along their pathway for collisions to produce the observed population of these light elements. One study suggested that it is about equivalent to passing through 4 cm of water.
One interesting aspect of cosmic rays is that they are almost totally matter rather than antimatter. According to Carroll & Ostlie, only about 0.01% of cosmic rays are antimatter, so this sample of the particles of our galaxy provides evidence of the matter-antimatter asymmetry in our galaxy and presumably in the universe as a whole. The few antiparticles that are observed can be accounted for as the results of high energy particle collisions that produce particle-antiparticle pairs.
High energy collisions in the upper atmosphere produce cascades of lighter particles. Pions and kaons are produced, which decay to produce muons. Muons make up more than half of the cosmic radiation at sea level, the remainder being mostly electrons, positrons and photons from cascade events.(Richtmyer)
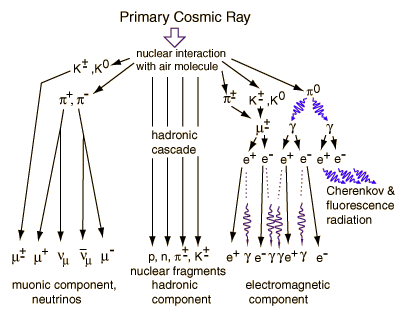

Sem comentários:
Enviar um comentário